最大似然估计
出自 MBA智库百科(https://wiki.mbalib.com/)
最大似然估计(Maximum Likelihood,ML)
目录 |
最大似然估计是一种统计方法,它用来求一个样本集的相关概率密度函数的参数。这个方法最早是遗传学家以及统计学家罗纳德·费雪爵士在1912年至1922年间开始使用的。
“似然”是对likelihood 的一种较为贴近文言文的翻译,“似然”用现代的中文来说即“可能性”。故而,若称之为“最大可能性估计”则更加通俗易懂。
最大似然法明确地使用概率模型,其目标是寻找能够以较高概率产生观察数据的系统发生树。最大似然法是一类完全基于统计的系统发生树重建方法的代表。该方法在每组序列比对中考虑了每个核苷酸替换的概率。
例如,转换出现的概率大约是颠换的三倍。在一个三条序列的比对中,如果发现其中有一列为一个C,一个T和一个G,我们有理由认为,C和T所在的序列之间的关系很有可能更接近。由于被研究序列的共同祖先序列是未知的,概率的计算变得复杂;又由于可能在一个位点或多个位点发生多次替换,并且不是所有的位点都是相互独立,概率计算的复杂度进一步加大。尽管如此,还是能用客观标准来计算每个位点的概率,计算表示序列关系的每棵可能的树的概率。然后,根据定义,概率总和最大的那棵树最有可能是反映真实情况的系统发生树。
给定一个概率分布D,假定其概率密度函数(连续分布)或概率聚集函数(离散分布)为fD,以及一个分布参数θ,我们可以从这个分布中抽出一个具有n个值的采样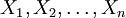 ,通过利用fD,我们就能计算出其概率:
,通过利用fD,我们就能计算出其概率:
但是,我们可能不知道θ的值,尽管我们知道这些采样数据来自于分布D。那么我们如何才能估计出θ呢?一个自然的想法是从这个分布中抽出一个具有n个值的采样X1,X2,...,Xn,然后用这些采样数据来估计θ.
一旦我们获得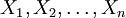 ,我们就能从中找到一个关于θ的估计。最大似然估计会寻找关于 θ的最可能的值(即,在所有可能的θ取值中,寻找一个值使这个采样的“可能性”最大化)。这种方法正好同一些其他的估计方法不同,如θ的非偏估计,非偏估计未必会输出一个最可能的值,而是会输出一个既不高估也不低估的θ值。
,我们就能从中找到一个关于θ的估计。最大似然估计会寻找关于 θ的最可能的值(即,在所有可能的θ取值中,寻找一个值使这个采样的“可能性”最大化)。这种方法正好同一些其他的估计方法不同,如θ的非偏估计,非偏估计未必会输出一个最可能的值,而是会输出一个既不高估也不低估的θ值。
要在数学上实现最大似然估计法,我们首先要定义可能性:
并且在θ的所有取值上,使这个[[函数最大化。这个使可能性最大的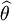 值即被称为θ的最大似然估计。
值即被称为θ的最大似然估计。
- 这里的可能性是指
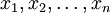 不变时,关于θ的一个函数。
不变时,关于θ的一个函数。
- 最大似然估计函数不一定是惟一的,甚至不一定存在。
考虑一个抛硬币的例子。假设这个硬币正面跟反面轻重不同。我们把这个硬币抛80次(即,我们获取一个采样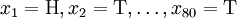 并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为p,抛出一个反面的概率记为1 − p(因此,这里的p即相当于上边的θ)。假设我们抛出了49个正面,31 个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为p = 1 / 3, p = 1 / 2, p = 2 / 3. 这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个可能性函数取以下三个值中的一个:
并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为p,抛出一个反面的概率记为1 − p(因此,这里的p即相当于上边的θ)。假设我们抛出了49个正面,31 个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为p = 1 / 3, p = 1 / 2, p = 2 / 3. 这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个可能性函数取以下三个值中的一个:
我们可以看到当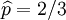 时,可能性函数取得最大值。这就是p的最大似然估计.
时,可能性函数取得最大值。这就是p的最大似然估计.
现在假设例子1中的盒子中有无数个硬币,对于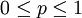 中的任何一个p, 都有一个抛出正面概率为p的硬币对应,我们来求其可能性函数的最大值:
中的任何一个p, 都有一个抛出正面概率为p的硬币对应,我们来求其可能性函数的最大值:
其中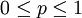 .
我们可以使用微分法来求最值。方程两边同时对p取微分,并使其为零。
.
我们可以使用微分法来求最值。方程两边同时对p取微分,并使其为零。
在不同比例参数值下一个二项式过程的可能性曲线 t = 3, n = 10;其最大似然估计值发生在其众数(数学)并在曲线的最大值处。
其解为p = 0, p = 1,以及p = 49 / 80. 使可能性最大的解显然是p = 49 / 80(因为p = 0 和p = 1 这两个解会使可能性为零)。因此我们说最大似然估计值为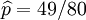 .
.
这个结果很容易一般化。只需要用一个字母t代替49用以表达伯努利试验中的被观察数据(即样本)的'成功'次数,用另一个字母n代表伯努利试验的次数即可。使用完全同样的方法即可以得到最大似然估计值:
对于任何成功次数为t,试验总数为n的伯努利试验。
其n个正态随机变量的采样的对应密度函数(假设其独立并服从同一分布)为:
或:
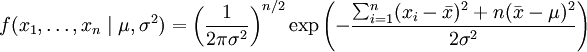 ,
,
这个分布有两个参数:μ,σ2. 有人可能会担心两个参数与上边的讨论的例子不同,上边的例子都只是在一个参数上对可能性进行最大化。实际上,在两个参数上的求最大值的方法也差不多:只需要分别把可能性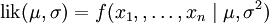 在两个参数上最大化即可。当然这比一个参数麻烦一些,但是一点也不复杂。使用上边例子同样的符号,我们有θ = (μ,σ2).
在两个参数上最大化即可。当然这比一个参数麻烦一些,但是一点也不复杂。使用上边例子同样的符号,我们有θ = (μ,σ2).
最大化一个似然函数同最大化它的自然对数是等价的。因为自然对数log是一个连续且在似然函数的值域内严格递增的函数。[注意:可能性函数(似然函数)的自然对数跟信息熵以及Fisher信息联系紧密。求对数通常能够一定程度上简化运算,比如在这个例子中可以看到:
这个方程的解是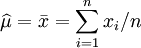 . 这的确是这个函数的最大值,因为它是μ里头惟一的拐点并且二阶导数严格小于零。
. 这的确是这个函数的最大值,因为它是μ里头惟一的拐点并且二阶导数严格小于零。
同理,我们对σ求导,并使其为零。
这个方程的解是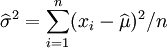 .
.
因此,其关于θ = (μ,σ2)的最大似然估计为:
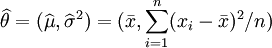 .
.
如果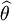 是 θ的一个最大似然估计,那么α = g(θ)的最大似然估计是
是 θ的一个最大似然估计,那么α = g(θ)的最大似然估计是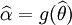 . 函数 g 无需是一个——映射。
. 函数 g 无需是一个——映射。
最大似然估计函数在采样样本总数趋于无穷的时候达到最小方差(其证明可见于Cramer-Rao lower bound)。当最大似然估计非偏时,等价的,在极限的情况下我们可以称其有最小的均方差。对于独立的观察来说,最大似然估计函数经常趋于正态分布。
最大似然估计的非偏估计偏差是非常重要的。考虑这样一个例子,标有1到n的n张票放在一个盒子中。从盒子中随机抽取票。如果n是未知的话,那么n的最大似然估计值就是抽出的票上标有的n,尽管其期望值的只有(n + 1) / 2. 为了估计出最高的n值,我们能确定的只能是n值不小于抽出来的票上的值。
最大似然估计的一般求解步骤[1]
基于对似然函数L(θ)形式(一般为连乘式且各因式>0)的考虑,求θ的最大似然估计的一般步骤如下:
(1)写出似然函数
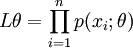 (总体X为离散型时)
(总体X为离散型时)
或 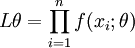 (总体X为连续型时)
(总体X为连续型时)
(2)对似然函数两边取对数有
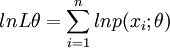
或 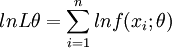
(3)对lnL\theta求导数并令之为0:
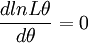
此方程为对数似然方程。解对数似然方程所得,即为未知参数 的最大似然估计值。
例1
设总体X~N(μ,σ2),μ,σ2为未知参数,X1,X2...,Xn是来自总体X的样本,X1,X2...,Xn是对应的样本值,求μ与σ2的最大似然估计值。
解 X的概率密度为
f(x;μ,σ2)=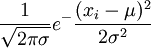 (
(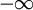 <x<+
<x<+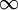 ),
),
可得似然函数如下:
L(μ,σ2)=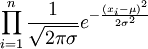
取对数,得
lnL(μ,σ2)=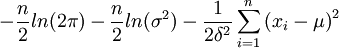
令
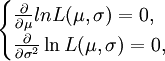
可得
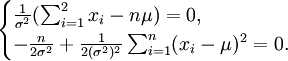
解得
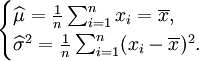
故μ和δ2的最大似然估计量分别为
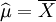 ,
,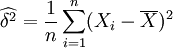
- ↑ 王翠香编著.概率统计.北京大学出版社,2010.02
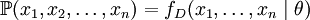
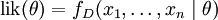
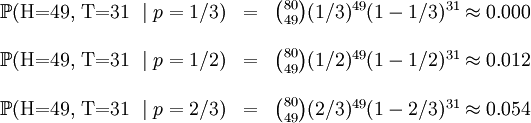
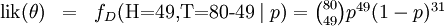
![\begin{matrix} 0 & = & \frac{d}{dp} \left( \binom{80}{49} p^{49}(1-p)^{31} \right) \\ & & \\ & \propto & 49p^{48}(1-p)^{31} - 31p^{49}(1-p)^{30} \\ & & \\ & = & p^{48}(1-p)^{30}\left[ 49(1-p) - 31p \right] \\ \end{matrix}](/w/images/math/f/4/3/f43c984e21445732edf403445fe32ea9.png)
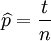
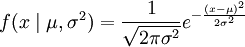
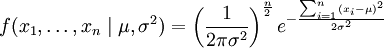
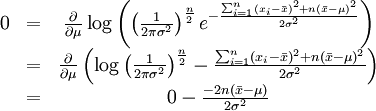
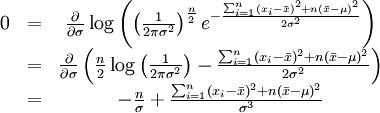








例子好难哦~ 不理解~ 哎 我太浅薄了