顺推归纳法

出自 MBA智库百科(https://wiki.mbalib.com/)

顺推归纳法(Forwards Induction)

　　顺推归纳法是指根据博弈方前面阶段的行为，包括偏离特定均衡路径的行为，推断他们的思路并为后面阶段博弈提供依据的分析方法。考虑的是博弈方有意识偏离子博弈精炼纳什均衡和颤抖手均衡路径的可能性，而不是偶然错误。

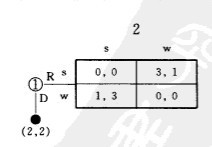
　　顺推归纳法是现实中的博弈方对相关问题可能有的其他理解和处理方法中最重要的一种。我们用右图van Damme(1989)提出的博弈例子说明顺推归纳法的思想。这个博弈第一阶段是博弈方1的选择阶段，博弈方1首先必须在D和R之间选择，如果他选择D，那么结束博弈，双方各得2；如果他选择R，则双方进行第二阶段的静态博弈。这个静态博弈有三个纳什均衡，即纯策略纳什均衡(S，w)和(w，S)，以及双方都以3／4和1／4的概率分布随机选择S和w的混合策略纳什均衡。注意如果进行第二阶段的静态博弈，那么上述三个纳什均衡给双方的平均得益明显小于2。

　　这个博弈的纳什均衡路径之一，是搏弈方1在第一阶段就选择D，而如果达到第二阶段的静态博弈(博弈方1自己在第一阶段实际选择了R)，双方再采用第二阶段静态博弈的纳什均衡(w，S)。容易验证，(Dw，S)是该博弈的子博弈完美纳什均衡，并且也是颤抖手均衡。

　　但对于(Dw，s)是否确实是这个博弈的具有稳定性的均衡是有疑问的。因为如果在这个博弈中博弈方1在第一阶段确实选择了R，那么显然有比博弈方1的选择是出了差错更有说服力的解释，那就是博弈方1是有意识这么选择的。如果把这个博弈表示成右图中的得益矩阵(或称策略形)形式就很容易理解这一点。根据该策略形不难明白一个理性的博弈方本身就是不会选择Rw的，因为它是严格下策，博弈方1在第一阶段选择R而不选择D，就是准备在第二阶段选择S。在这样的判断下，博弈方2在第二阶段的最佳选择就只有w。如果博弈方1相信博弈方2有分析能力，就可以预计到博弈方2的推理，知道自己第一阶段选择R，有把握在第二阶段实现对自己比较有利的均衡(S，w)，这当然比第一阶段直接选择D更有利。因此既是子博弈完美纳什均衡，又是颤抖手均衡的(Dw，S)，实际上是不稳定的。在这个博弈中真正具有稳定性，比较可能出现的均衡，是另一个子博弈完美纳什均衡和颤抖手均衡(Rs，w)。

　　上述分析说明了颤抖手均衡的思想方法确实并不能完全解决动态博弈中均衡的精炼问题。上述根据博弈方前面阶段的行为，包括偏离特定均衡路径的行为，推断他们的思路并为后面阶段博弈提供依据的分析方法，就是“顺推归纳法”。顺推归纳法考虑的是博弈方有意识偏离子博弈完美纳什均衡和颤抖手均衡路径的可能性，而不是偶然性的错误。顺推归纳法是精练纳什均衡的另一种重要的方法。