积分第一中值定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
积分第一中值定理是积分中值定理的推广之一,此外还有积分第二中值定理。积分中值定理揭示了一种将积分化为函数值, 或者是将复杂函数的积分化为简单函数的积分的方法。是数学分析的基本定理和重要手段, 在求极限、判定某些性质点、估计积分值等方面应用广泛。
设 ![f:[a,b]\rightarrow \mathbf R](/w/images/math/6/3/f/63faa29e7424e4f0bb11573e77db61f1.png) 为一连续函数,
为一连续函数,![g:[a,b]\rightarrow \mathbf R](/w/images/math/1/7/f/17fcc207ca60db3468a647c7a3436214.png) 为一正的可积函数,那么存在一点
为一正的可积函数,那么存在一点 ![\xi\in [a,b]](/w/images/math/f/8/3/f83ba3f626ed0ec9d1df2f3139d398d0.png) 使得
使得
如果函数 在闭区间 上连续, 在 上不变号,并且 在闭区间 上是可积的,则在 上至少存在一个点 ,使下式成立:
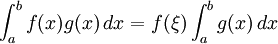 。
。
事实上,可以证明,上述的中值点ξ必能在开区间(a,b)内取得,见下方中值点在开区间内存在的证明。
因为 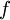 是闭区间上的连续函数,
是闭区间上的连续函数,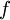 取得最大值
取得最大值 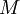 和最小值
和最小值 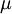 。于是
。于是
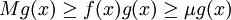 。
。
对不等式求积分,我们有
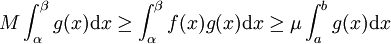 。
。
若 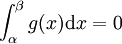 ,则
,则 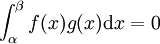 。
。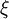 可取
可取 ![[\alpha,\beta]\](/w/images/math/9/f/e/9fe4f17a1e12a0215ff8fa3cb7a1d963.png) 上任一点。
上任一点。
设 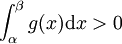 ,那么
,那么
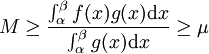 。
。
因为 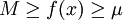 是连续函数,则必存在一点
是连续函数,则必存在一点 ![\xi\in[\alpha,\beta]](/w/images/math/4/5/c/45c131d54bb2d936cfad0ffdbbfa0df6.png) ,使得
,使得
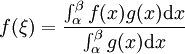 。
。
已知f(x)在[a,b]上连续,设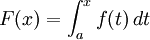 。
。
知F(x)在[a,b]上连续,在[a,b]内可导,应用拉格朗日中值定理,可得:
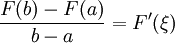 ,其中
,其中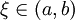
即
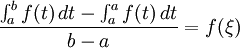
所以
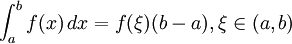 。
。







