密切值法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什么是密切值法

　　密切值法是系统工程中多目标决策的一种优选方法。多目标决策由于考虑的目标多，标准多，有些目标之间还存在着矛盾，这就使多目标问题成为一个复杂而困难的问题，密切值法是解决有限方案多目标决策的有效方法。从整个决策过程来看，多目标决策与评价是同一概念，这里的决策实质上就是分析和评价过程。密切值法计算灵活简便，结果直观明了，分辨率较高，近几年来已广泛应用于经济、社会、医学、环保等领域，是综合评价的一种行之有效的方法。

[编辑]

密切值法的基本原理

　　对于同时存在正向指标(即数值越高越好，如治愈率)和负向指标(即数值越低越好，如病死率)的决策评价系统，将其转化为同向指标(同正向或同反向)系统，然后找出各评价指标的“最优点”和“最劣点”，通过计算各评价对象与“最优点”及“最劣点”的距离，以其密切值的大小排出各评价对象的优劣顺序。

[编辑]

密切值法的基本步骤

　　1)建立原始数据指标矩阵：设有n个评价对象，每个评价对象有m个评价指标，将原始数据写成指标矩阵

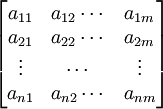
　　 $\begin{bmatrix}a_{11}& a_{12}\cdots & a_{1m}\\a_{21}& a_{22}\cdots & a_{2m}\\\vdots &\cdots &\vdots\\a_{n1}& a_{n2}\cdots & a_{nm}\end{bmatrix}$

　　2)建立同向指标矩阵：当评价指标为正向指标时，数值取正值；当评价指标为负向指标时，数值取负值，得同向指标矩阵

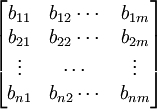
　　 $\begin{bmatrix}b_{11}& b_{12}\cdots & b_{1m}\\b_{21}& b_{22}\cdots & b_{2m}\\\vdots &\cdots &\vdots\\b_{n1}& b_{n2}\cdots & b_{nm}\end{bmatrix}$

　　3)建立标准化矩阵

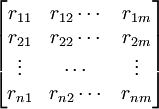
　　 $\begin{bmatrix}r_{11}& r_{12}\cdots & r_{1m}\\r_{21}& r_{22}\cdots & r_{2m}\\\vdots &\cdots &\vdots\\r_{n1}& r_{n2}\cdots & r_{nm}\end{bmatrix}$

　　其中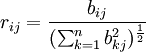， $r_{ij}=\frac{b_{ij}}{(\sum_{k=1}^n b^2_{kj})^{\frac{1}{2}}}$

　　i=1,2,…,n；j=1,2,…,m。

　　4)确定“最优点”和“最劣点”

　　最优点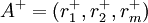 $A^{+}=(r_1^{+},r_2^{+},r_m^{+})$

　　最劣点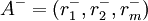 $A^{-}=(r_1^{-},r_2^{-},r_m^{-})$

　　其中，

　　5)计算各评价对象到“最优点”与“最劣点”的距离

　　 $d_i^{+}=[\sum_{j=1}^m(r_{ij}-r_j^{+})^2]^{\frac{1}{2}}]$

　　 $d_i^{-}=[\sum_{j=1}^m(r_{ij}-r_j^{-})^2]^{\frac{1}{2}}$

　　i=1,2,…,n；j=1,2,…,m。

　　6)计算各评价对象的“密切值”，并据此排出优劣顺序

　　密切值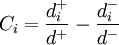 $C_i=\frac{d_i^{+}}{d^{+}}-\frac{d_i^{-}}{d^{-}}$ 　i=1,2,…,n

　　其中，

　　当密切值 $C i$ 越小时，与“最优点”越密切，与“最劣点”越疏远，即质量越高。 $C i = 0$ 时，质量最佳，即为“最优点”。

[编辑]

密切值法的实例分析^[1]

　　实例:。永安渠首工程规划选择了3个方案,即坝线位置为下坝线,永安进水闸以上4·3km为中坝线,永安进水闸以上6·2km即诺敏河口以下800m为上坝线。各方案(上坝线为第1方案、中坝线为第2方案、下坝线为第3方案)技术经济指标的数据如表1所示。

　　表1　各方案技术经济指标数据

指标方案	闸坝(万元)	固滩(万元)	引渠(万元)	引水条件	滩地状况	安全性	管理运用
1	731	302	554	0.45	0.70	0.95	0.40
2	733	305	365	0.85	0.70	0.95	0.85
3	756	431	156	0.60	0.45	0.50	0.40

　　渠首工程方案选择的前题是:投资少,引水条件合理,滩地状况良好,安全可靠及管理方便。因此,上述指标中,引水条件、滩地状况、安全性、管理运用都是正向指标,闸坝、固滩、引渠都为负指标。按式计算 $r i j$ ,将其结果列于表2。由(2)和(3)得“最优点” $A +$ 和“最劣点” $A -$

$A +$ =(-0.570 3,-0.496 4,-0.228 9,0.749 8,0.643 7,….662 7,0.832 5)

$A -$ =(-0.589 8,-0.708 6,-0.812 9,0.397 0,0.413 8,0.348 8,0.391 8)

　　表2　规范化指标矩阵

指标方案	闸坝(万元)	固滩(-)	引渠(-)	引水条件(+)	滩地状况(+)	安全性(+)	管理运用(+)
1	-0.5703	-0.4964	-0.8129	0.3970	0.6437	0.6627	0.3918
2	-0.5719	-0.5014	-0.5356	0.7498	0.6637	0.6627	0.8325
3	-0.5898	-0.7086	-0.2289	0.5293	0.4138	0.3488	0.3918

　　计算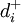 $d_i^{+}$ 和 $d_i^{-}$

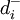
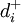　　 $d_i^{+}$ =(0.812 3,0.306 7,0.663 0),

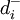　　 $d_i^{-}$ =(0.443 6,0.768 2,0.598 8)

　　则

　　得密切值

　　 $C i = (2.0710,0,1.3822)$

　　由于 $C 2 < C 3 < C 1$ ,说明方案2为最佳方案,即永安渠首规划方案应选中坝线。

[编辑]

参考文献

↑ 何东进,洪伟,林改平,朱忠泰,莫明玉.多目标决策的密切值法及其应用研究[J].《农业系统科学与综合研究》.2001,02

来自"https://wiki.mbalib.com/wiki/%E5%AF%86%E5%88%87%E5%80%BC%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

Yixi,LuyinT.

页面分类: 硬评价方法

评论(共1条)

提示:评论内容为网友针对条目"密切值法"展开的讨论，与本站观点立场无关。

218.65.113.* 在 2014年7月13日 15:48 发表

回复评论

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

密切值法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是密切值法

密切值法的基本原理

密切值法的基本步骤

密切值法的实例分析^[1]

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共1条)

导航

意见反馈

查看

工具箱▼

密切值法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是密切值法

密切值法的基本原理

密切值法的基本步骤

密切值法的实例分析[1]

参考文献

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共1条)

导航

意见反馈

密切值法的实例分析^[1]