几何级数增长
出自 MBA智库百科(https://wiki.mbalib.com/)
几何级数增长(geometric growth)
目录 |
几何级数增长就是成倍数增长。类似与通常说的“翻番”——2、4、8、16、32、64、128等等,或者3、9、27、81等等。在几何上,面积与边长的关系是乘积的函数关系。因此也将成倍增长称为“几何级数增长”。
案例一:种群的几何级数增长[1]
在具体讨论现实的种群在有限的环境中增长过程以前,首先介绍一个理想的种群在无限的环境中增长的模型。假定有一种一年只有一个繁殖季、寿命只有一年的动物,那么其世代是不重叠的。例如,栖居于草原季节性小水坑中的水生昆虫,每年雌虫产一次卵,卵孵化长成幼虫,蛹在泥中度过干旱季节。到第二年,蛹才变为成虫,交配、产卵。因此,世代是不重叠的,种群增长是不连续的。假定这些水坑是彼此隔离的,即种群没有迁入和迁出。
1.模型的假设和概念结构
在这个最简单的单种种群增长模型的概念结构里,包含有下列四个假设:①种群增长是无界的,即设种群在无限的环境中增长,没有受资源、空间等条件的限制;②世代不相重叠。增长是不连续的,或称离散的;③种群没有迁入和迁出;④没有年龄结构。
2.数学模型
最简单的单种种群增长的数学模型通常是把世代t+1的种群Nt + 1与世代t的种群Nt联系起来的差分方程:式中:N为种群大小,t为时间,λ为种群的周限增长率。
3.模型的生物学含义
下面我们对这个模型的生物学含义作进一步解释。
假定一年生生物(即世代间隔为一年)的种群在一个繁殖季节t0开始,有N0个雌体和等量的雄体(这样就能简单地以雌体产生雌体来代表种群增长),其产卵量为B,总死亡为D。那么到下一年t1,其种群数量N1为如果种群在无限环境下以这个速率年复一年地增长,即
N0 = 10
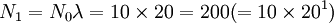
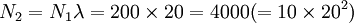

……
Nt + 1 = Ntλ或Nt = N0λ'
λ在此是表示种群以每年(或其他时间单位)为前1年20倍的速率而增长的增长率,称为周限增长率。这种增长形式称为几何级数式增长或指数式增长。
将方程式Nt = N0λ'两侧取对数,即它具有直线方程式y=a+bx的形式。因此,以lgNt与t作图,就能得到一条直线,其中lgN0是直线的截距,lgλ是直线的斜率。
4.模型的参数λ
周限增长率λ是种群增长模型中有用的量,如果λ = Nt + 1 / Nt = 1,表示种群数量在t时和t+1时相等,种群稳定。从理论上讲,λ可以有下面四种情况,它在种群增长中的含义是:
λ>1,种群上升;
λ=1,种群稳定;
0<λ<1,种群下降;
λ=0,雌体没有繁殖,种群在一代中灭亡。
- ↑ 林文雄主编.生态学.科学出版社,2007.8.







