偏心质量
出自 MBA智库百科(https://wiki.mbalib.com/)
偏心质量(Eccentric Mass)
目录 |
什么是偏心质量[1]
偏心质量是指偏心轮安装偏心块处的“多余”(较之未安装偏心块处)金属的质量与偏心块质量之和。
偏心质量引起的强迫振动[2]
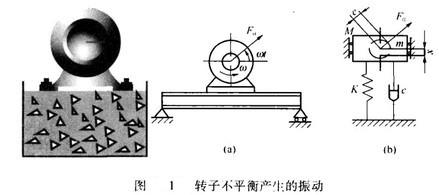
旋转机械设备,如电机、离心泵、离心压缩机、通风机和汽轮机等的转动部件,通常称为转子。由于转子的偏心质量而引起振动的现象是很普遍的。如果激振力是因转子的不平衡而产生的,则与简谐激振力直接作用于质量块上的情况就不完全一样。引发不平衡情况发生的原因有许多,如转子的制造、安装过程中的误差、材质不均匀,都将使质心位置偏离转子的回转中心线。转子旋转时产生不平衡离心力,引起动不平衡,机器因此强迫振动。当考虑转子的弹性时,不平衡力将引起转子的弯曲,产生动挠度。当转速在数值上等于转子不转动而做横向自由振动的固有频率时,转子的动挠度和轴承支承处的动反力在理论上趋于无穷大(实际受阻尼的限制只会很大),作用在轴承上的交变力导致支承系统发生强迫振动,引起机器的共振。下面将对旋转机械中转子因偏心质量不平衡而引起的强迫振动进行研究讨论。
- 1.运动微分方程的建立
 (2)
(2)
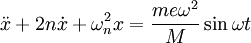 (3)
(3)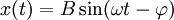 (4)
(4)
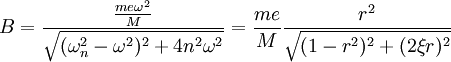 (5)
(5)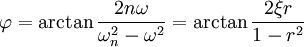
- 2.幅频响应曲线和相频响应曲线
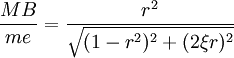 (6)
(6) 为纵坐标(与振幅成定比)亦可根据不同的ξ值得出一组曲线,即幅频响应曲线组,如图2所示。由图可看出与前述幅频响应曲线有两个不同特点:
为纵坐标(与振幅成定比)亦可根据不同的ξ值得出一组曲线,即幅频响应曲线组,如图2所示。由图可看出与前述幅频响应曲线有两个不同特点: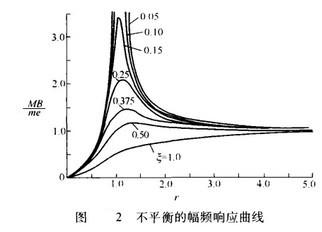
(1)当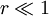 时(
时(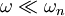 ),振幅B很小,几乎等于零。显然,马达低转速时激振力F0 = meω2很小。
),振幅B很小,几乎等于零。显然,马达低转速时激振力F0 = meω2很小。
(2)当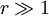 时(
时(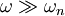 ),
), →1,B→
→1,B→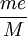 ,即在高频范围内,振幅接近于常数,并不是趋于零。
,即在高频范围内,振幅接近于常数,并不是趋于零。
(3)当r=1时,产生共振,振幅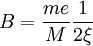 ,系统振动激烈。
,系统振动激烈。
一个实际系统的阻尼系数是不容易计算的,按上面这个特点,可用试验方法测定阻尼系数。首先测定共振r=1时振幅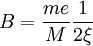 ,算得阻尼系数
,算得阻尼系数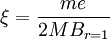 ,再测定
,再测定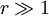 时的振幅,即
时的振幅,即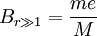 便可求出阻尼系数
便可求出阻尼系数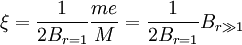 。
。







