低劣化数值法
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
[编辑]
什么是低劣化数值法[1]
低劣化数值法是假定设备使用后残值为零，设备维护修理费及燃料动力费每年以固定数值增加的条件下，以年平均设备费用最低为标准，确定设备最优更新期的一种方法。
[编辑]
低劣化数值法的计算及举例[2]
设K0代表设备的原始价值，O代表设备更新时的残值，T代表设备已使用的年限，则每年平均分摊的设备费用为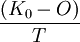
。
随着T的增长，按年平均的设备费用不断减少，但设备的维护修理费用及燃料、动力消耗增加，这就叫设备的低劣化。若这种低劣化每年以A的数值增加，则第T年的低劣化数值为λT，第T年中平均低劣化数值为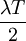
。由此可得平均每年的设备费用总和为：
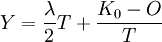
若使设备费用最小，则取：
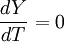,得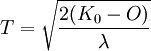
如果不考虑残值，则可简化为：
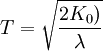
例：某设备的原始价值为K0=16000元，每年低劣化增加值λ=500元，则在不考虑残值的情况下，最佳更新年限为：
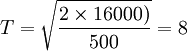(年)
或者用以下的方法，在λ和K0已知的条件下，按使用年限的顺序代入
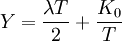
则可得到下表：
| 使用年限T | 设备费用 | 年均低劣化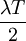 | 合计 |
| 1 | 16000 | 250 | 16250 |
| 2 | 8000 | 500 | 8500 |
| 3 | 5333 | 750 | 6083 |
| 4 | 4000 | l000 | 5000 |
| 5 | 3200 | l250 | 4450 |
| 6 | 2666 | l500 | 4166 |
| 7 | 2285 | 1750 | 4035 |
| 8 | 2000 | 2000 | 4000 |
| 9 | l777 | 2250 | 4027 |
| lO | l600 | 2500 | 4100 |
| 11 | 1454 | 2750 | 4204 |
从表中可见，第8年的总费用最低，第8年为经济使用年限，7～9年总费用差别不大，故此区间三个年限为最佳更换年限。
如果考虑残值，假设该设备的残值为4000元，则其最佳更换年限为：
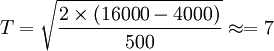(年)
[编辑]
