九宫图分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
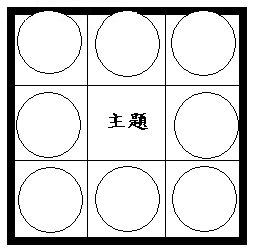
九宫图法是一种有助扩散性思维的思考策略,利用一幅像九宫格图,如下图所示,将主题写在中央,然后把由主题所引发的各种想法或联想写在其余优点乃由事物之核心出发,向八个方向去思考,发挥八种不同的创见。依循此思维方式加以发挥并扩散其思考范围。
九宫图
(一)曼陀罗法
曼陀罗法是一种有助扩散性思维的思考策略,利用一幅像九宫格图,将主题写在中央,然后把由主题所引发的各种想法或联想写在其余的八个圈内,此法也可配合六何法从多方面进行思考。
[备注]:此九宫格法可作为扩散性思维的基本单位,由此演变出其它九宫格法(如莲花法中央的单位,正是曼陀罗法的基本单位)。此法之优点乃由事物之核心出发,向八个方向去思巧,发挥八种不同的创见。而莲花法也是依循此思维方式加以发挥并扩散其思考范围。
(二)莲花法
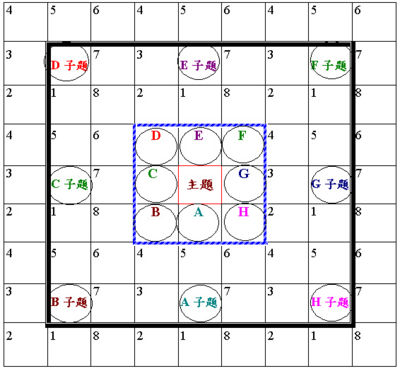
这是从曼陀罗法的基本单位发展扩展而来(下图)。
莲花法图
(1) 每位讨论者手持一莲花图,并将讨论之主题或问题写于图中央位置。
(2) 把相关的意念写于围着主题四周的八个圈中(每个圈的左上角分别写上英文字母A至H),成为八个子题,并于图中央部分构成了一幅曼陀罗法九宫图。随后,讨论者可就各个子题再想出另外八个意念,将之写于围着「子题」四周及标着1-8号码的方格内,讨论者可沿以上步骤再延伸构思新的意念。
(3) 讨论直至整个莲花图写满为止。
(1)九宫数图起源
目前普遍认为,九宫数图即为“洛书”的主要内容,是最早关于数的起源之说(见图3)。《周易•系辞上》说:“河出图,洛出书,圣人则之。”[1]但其中并没有明确记载“洛书”的主要内容。直至西汉经学家孔安国的《尚书•洪范传》才提到:“天与禹,洛出书。神龟负文而出列于背,皆有数至于九。禹遂因而第之,以成九类,常道所以次序。” 刘歆注1云:“伏羲氏继天而王,受河图而画之,八卦是也。禹治洪水,赐洛书,法而陈之,九畴是也。” 其九畴,即“戴九履一,左三右七,二四为肩,六八为足,五居中央,正龟背之象也”。[2]
《周易本经》的洛书图解
据《史记•夏本纪》记载:夏禹治水时,“左准通,右规矩,载四时,以开九州,通九道,陈九泽……”。此后大禹以洛书为据,应用到测量、气象、地理与交通运输之中,从而治理黄河,大获成功。由于神龟所背图是在黄河支流洛水中发现,且图中内容如书一样深奥,故称之为洛书。
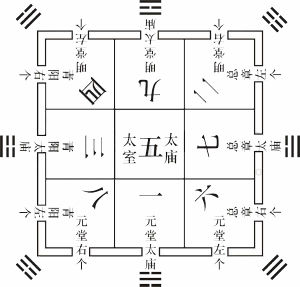
而九宫之说首见于《大戴礼记•明堂篇》,其中言到,明堂有“九室”(见下图),其形上圆下方,其数为:“二四九,七五三,六一八。”其中所记载的九畴、祠庙、太庙、明堂等建筑都用此方法。之后,九宫结构多被用于皇帝的宫室中。《管子•幼官》、《吕氏春秋•十二纪》、《礼记•月令》等典籍中都有关于天子在一年四季分居九个不同宫室的记载。[3]
明堂九室图
后人根据九宫数图创造了“九宫算”的计算方法,我国后汉徐岳的《数术记遗》一书中已有记载:“九宫算注2, 五行参数, 犹如循环, 九宫者, 即二四为肩, 六八为足, 左三右七, 戴九履一, 五居中央。”[4]
(2)九宫数图内在的排列规律
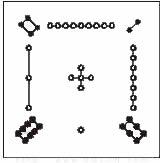
九宫数图既是一种组合计算,又是一种益智游戏。后来形成的“九宫算”及“排九宫”等都是以九宫数图为基础(见下图)。
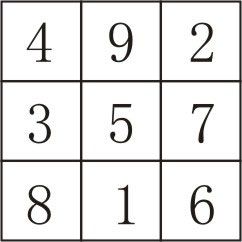
九宫数图
九宫数图最基本的规律,是其纵横及对角线上三数之和都为15,且九个数相加之和为45,是15的3倍。深入研究其数字的排列组合,可以发现以下规律:
①其8组数列中包含4组等差数列:[4、5、6] 、[3、5、7]、 [8、5、2] 、[1、5、9],以5为中心,逆时针方向,各数列的公差分别为1、2、3、4,又是一个以1为公差的等差数列(如下图所示);
九宫数图中的数列
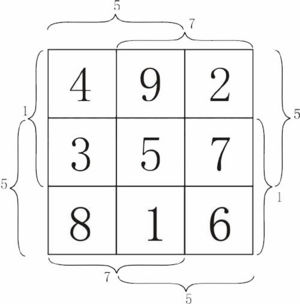
②另四组数列也有一定的规律(如下图所示),从图中可以看出,这四个数列相邻两数的差颠倒对称,而且四边的数中,均有相邻两数之差为5,且各个数字均不重复,具体为:上[4、9、2]9-4=5;下[8、1、6]6-1=5;左[4、3、8]8-3=5;右[2、7、6]7-2=5;
九宫数图
③奇数和偶数相互交错排列,四角之数为偶数,中间之数为奇数,同时,中间除5之外的四个数,任何两个之差都为偶数,且分别为四角四个数,具体为:9-7=3-1=2;9-3=7-1=6;9-1=8;7-3=4(如下图所示)。
九宫数图
注释:
- 注1:孔安国:字子国,孔子十一代孙,西汉经学家;刘歆:字子发,汉宗室刘向之子,对于数术方技颇有研究,为中国研究求圆周率之第一人。
- 注2:“九宫算”是指以九宫数图为基础的计算方法,是指世界上最早出现的数学智力游戏,后来发展到“排九宫”,就是人们将9 块分别写有自然数1—9的正方形棋子在九宫格中布阵来构造三阶幻方,是世界上最早出现的几何形块的玩具。
评论(共44条)
一个有趣的排列组合数学游戏,但是我没从中发现这样的一种扩散性分析方法如果在这个图中得到真正的运用,它与我们常用到的头脑风暴法有什么实质上的区别。
好像没什么用的,对于数独!
如过三边加起来是16??
那该这么半啊
不可能 1+2+·····+9=45,每一组由3个数组成,so45*3只能=15
如过三边加起来是16??
那该这么半啊
怎样列出九宫图标
什么吗?会点小九宫就如此,如果你会中宫6x6及直线6个术的和lll,大九宫9x9及直线9人术的和369,相知道怎么做的吗?










如过三边加起来是16??
那该这么半啊