三线性插值
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
三线性插值是在三维离散采样数据的张量积网格上进行线性插值的方法。这个张量积网格可能在每一维度上都有任意不重叠的网格点,但并不是三角化的有限元分析网格。这种方法通过网格上数据点在局部的矩形棱柱上线性地近似计算点 (x,y,z) 的值。
三线性插值经常用于数值分析、数据分析以及计算机图形学等领域。
- 三线性插值在一次n=1三维D=3(双线性插值的维数为:D=2,线性插值:D=1)的参数空间中进行运算,这样就
需要(1 + n)D = 8个与所需插值点相邻的数据点。
- 三线性插值等同于三维张量的一阶B样条插值。
- 三线性插值运算是三个线性插值运算的张量积。
实例
在一个步距为1的周期性立方网格上,取
xd,yd,zd
为待计算点距离小于
x,y,z,
的最大整数的差值,即,
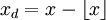
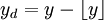
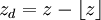
首先沿着z轴插值,得到:
![i_1=v\left[\left\lfloor x\right\rfloor,\left\lfloor y\right\rfloor\left\lfloor z\right\rfloor\right],\times(1-z_d)+v\left[\left\lfloor x\right\rfloor,\left\lfloor y\right\rfloor\left\lfloor z\right\rfloor\right]\times z_d](/w/images/math/9/1/2/912c833cc681ccc27296109ebf19607c.png)
![i_2=v\left[\left\lfloor x\right\rfloor,\left\lfloor y\right\rfloor\left\lfloor z\right\rfloor\right],\times(1-z_d)+v\left[\left\lfloor x\right\rfloor,\left\lfloor y\right\rfloor\left\lfloor z\right\rfloor\right]\times z_d](/w/images/math/d/e/9/de9263f0b399c3f6f6e34bdf8dd776c4.png)
![j_1=v\left[\left\lfloor x\right\rfloor,\left\lfloor y\right\rfloor\left\lfloor z\right\rfloor\right],\times(1-z_d)+v\left[\left\lfloor x\right\rfloor,\left\lfloor y\right\rfloor\left\lfloor z\right\rfloor\right]\times z_d](/w/images/math/0/c/e/0ce1989811ddecea5f6da79a7e8d4563.png)
![j_2=v\left[\left\lfloor x\right\rfloor,\left\lfloor y\right\rfloor\left\lfloor z\right\rfloor\right],\times(1-z_d)+v\left[\left\lfloor x\right\rfloor,\left\lfloor y\right\rfloor\left\lfloor z\right\rfloor\right]\times z_d](/w/images/math/7/d/a/7da933583f85f59352a5e1acaeb2d9d9.png)
然后,沿着y轴插值,得到:
w1 = i1(1 − yd) + i2yd
w2 = j1(1 − yd) + j2yd
最后,沿着x轴插值,得到:
IV = w1(1 − xd) + w2xd
这样就得到该点的预测值。
三线性插值的结果与插值计算的顺序没有关系,也就是说,按照另外一种维数顺序进行插值,例如沿着 x、 y、z 顺序插值将会得到同样的结果。这也与张量积的交换律完全一致。







