高斯積分

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是高斯積分

　　高斯積分是指依德國數學家兼物理學家卡爾•弗里德里希•高斯之姓氏所命名。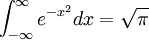 $\int_{-\infty}^\infty e^{-x^2}dx = \sqrt{\pi}$ 高斯積分在概率論和連續傅里葉變換等的統一化等計算中有廣泛的應用。在誤差函數的定義中它也出現。雖然誤差函數沒有初等函數，但是高斯積分可以通過微積分學的手段解析求解。

[編輯]

高斯積分的內容

　　任何高斯函數的積分均可簡化為含高斯積分的項。

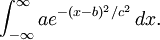
　　 $\int_{-\infty}^{\infty} ae^{-(x-b)^2/c^2}\,dx.$

　　常數 $a$ 可以被提出積分。使用 $y + b$ 來取代 $x$ 獲得

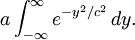
　　 $a\int_{-\infty}^\infty e^{-y^2/c^2}\,dy.$

　　使用 $c z$ 來取代 $y$ 取得

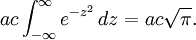
　　 $ac\int_{-\infty}^\infty e^{-z^2}\,dz=ac\sqrt{\pi}.$

[編輯]

高斯積分通過極限求解

　　要找到高斯積分的閉合形式首先從一個近似函數開始：

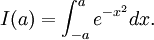
　　 $I(a)=\int_{-a}^a e^{-x^2}dx.$

　　通過

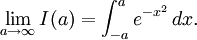
　　 $\lim_{a\to\infty} I(a) = \int_{-a}^a e^{-x^2}\, dx.$

　　可以找到積分。對 $I$ 取平方獲得

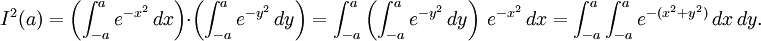
　　 $I^2(a)= \left ( \int_{-a}^a e^{-x^2}\, dx \right )\cdot \left ( \int_{-a}^a e^{-y^2}\, dy \right )= \int_{-a}^a \left ( \int_{-a}^a e^{-y^2}\, dy \right )\,e^{-x^2}\, dx = \int_{-a}^a \int_{-a}^a e^{-(x^2+y^2)}\,dx\,dy.$

　　使用富比尼定理以上雙重積分可以被看作是直角坐標繫上一個頂點為{(−a, a), (a, a), (a, −a), (−a, −a)}的正方形的面積積分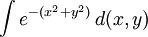 $\int e^{-(x^2+y^2)}\,d(x,y)$ 。

　　由於對任何實數來說指數函數均大於0，因此對於這個正方形內的內切圓的積分必須小於 $I (a) 2$ 。類似地正方形的外接圓積分必須大於 $I (a) 2$ 。通過從直角坐標系轉化到極坐標系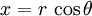 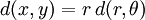$x=r\,\cos \theta$ , $y= r\,\sin\theta$ , $d(x,y) = r\, d(r,\theta)$ 對這兩個圓面的積分可以簡單地計算出來：

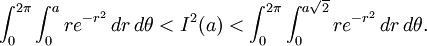
　　 $\int_0^{2\pi}\int_0^a re^{-r^2}\,dr\,d\theta < I^2(a) < \int_0^{2\pi}\int_0^{a\sqrt{2}} re^{-r^2}\,dr\,d\theta.$

　　對

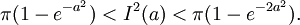
　　 $\pi (1-e^{-a^2}) < I^2(a) < \pi (1 - e^{-2a^2}).$

　　積分。

　　使用夾擠定理獲得高斯積

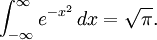
　　 $\int_{-\infty}^\infty e^{-x^2}\, dx = \sqrt{\pi}.$

[編輯]

高斯積分與Γ函數的關係

　　由於被積分的函數是一個奇函數與偶函數|偶函數，

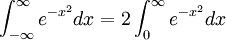
　　 $\int_{-\infty}^{\infty} e^{-x^2} dx = 2 \int_0^\infty e^{-x^2} dx$

　　通過替代變數它可以變成一個歐拉積分

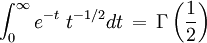
　　 $\int_0^\infty e^{-t} \ t^{-1/2} dt \, = \, \Gamma\left(\frac{1}{2}\right)$

　　這裡Γ是Γ函數。這說明瞭為什麼一個半整數的階乘是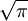 $\sqrt \pi$ 地倍數。更廣義地，

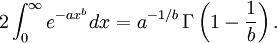
　　 $2\int_0^\infty e^{-ax^b} dx = a^{-1/b} \, \Gamma\left(1-\frac{1}{b}\right).$

[編輯]

高斯積分的n維和一般化

　　令 $A$ 為一個對稱的、正的、可逆的、二維協變的張量，則

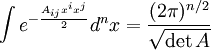
　　 $\int e^{-\frac{A_{ij} x^i x^j}{2}} d^nx=\frac{(2\pi)^{n/2}}{\sqrt{\det{A}}}$

　　這裡的積分是對Rⁿ的。這個事實可用來研究多元正態分佈。

　　同樣，

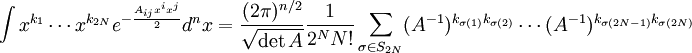
　　 $\int x^{k_1}\cdots x^{k_{2N}} e^{-\frac{A_{ij} x^i x^j}{2}} d^nx=\frac{(2\pi)^{n/2}}{\sqrt{\det{A}}}\frac{1}{2^N N!}\sum_{\sigma \in S_{2N}}(A^{-1})^{k_{\sigma(1)}k_{\sigma(2)}}\cdots (A^{-1})^{k_{\sigma(2N-1)}k_{\sigma(2N)}}$

　　這裡σ是{1, ..., 2N}的排列。右側的特殊因數是A⁻¹的 $N$ 個{1, ..., 2N}的成對的結合。

　　或者，

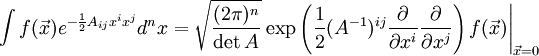
　　 $\int f(\vec{x})e^{-\frac{1}{2}A_{ij}x^i x^j} d^nx=\sqrt{(2\pi)^n\over \det{A}}\left. \exp\left({1\over 2}(A^{-1})^{ij}{\partial \over \partial x^i}{\partial \over \partial x^j}\right)f(\vec{x})\right|_{\vec{x}=0}$

　　以上積分適合於一些符合在其增長上有一定限度的和其他技術要求的解析函數。對微分運算元上的冪被看作是一個冪級數。

　　一般函數積分沒有明確的定義，但是高斯積分可以類似有限維情況被定義。雖然如此依然有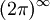 $(2\pi)^\infty$ 無窮大的問題，而且函數行列式一般也無窮大。但假如我們只考慮

　　 $\frac{\int f(x_1)\cdots f(x_{2N}) e^{-\iint \frac{A(x_{2N+1},x_{2N+2}) f(x_{2N+1}) f(x_{2N+2})}{2} d^dx_{2N+1} d^dx_{2N+2}} \mathcal{D}f}{\int e^{-\iint \frac{A(x_{2N+1},x_{2N+2}) f(x_{2N+1}) f(x_{2N+2})}{2} d^dx_{2N+1} d^dx_{2N+2}} \mathcal{D}f},$

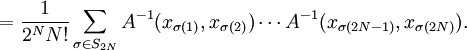
　　 $=\frac{1}{2^N N!}\sum_{\sigma \in S_{2N}}A^{-1}(x_{\sigma(1)},x_{\sigma(2)})\cdots A^{-1}(x_{\sigma(2N-1)},x_{\sigma(2N)}).$

　　這個問題可以解決。

　　使用德維特寫法這個公式與有限維情況看上去一樣。

[編輯]

高斯積分帶線性項的n維

　　A依然是一個對稱矩陣，則

　　 $\int e^{-A_{ij} x^i x^j+B_i x_i} d^nx=\sqrt{ \frac{\pi^n}{\det{A}} }e^{\frac{1}{4}B^TA^{-1}B}.$

[編輯]

高斯積分提出者人物簡介

　　德國布隆斯威克人。德國的數學家、物理學家和天文學家。高斯幼年時就顯示出非凡的數學才能，得到Carl Wil-helm Ferdinand大公的賞識。在大公的支持下，1795—1798年在哥廷根(Gottingen)大學學習，1799年因證明代數學的基本定理而獲得哈勒(Halle)大學的博士學位。從1807年到1855年逝世，一直擔任哥廷根天文臺台長兼大學教授。1796年用直尺圓規作出了正十七邊形一自歐幾裡得以來兩千年間幾何作圖的一個難題。接著又證明瞭數論中的歐勒猜想—二次互反律。據說從此後他決心放棄古典文學而獻身於數學。1801年用自己的行星軌道計稱法和最小二乘法算出了義大利天文學家皮亞齊 (1746—1826) 發現的穀神星軌道; 穀神星的軌道計算使他一舉名震世界。同年，出版經典著作《算術研究》，任職期間，高斯致力於數論、代數、幾何、分析、複變函數、統計數學等多方面的研究、取得了一系列的成果。高斯定理、高斯公式、高斯函數等以他命名的多種發現至今仍在許多數學、科學部門中閃爍著光輝。高斯還涉足了大地測量工作。為了進行長距離測量，發明瞭“目光反射器”，併在理論上創造了“大地問題解法”，導致他開創了曲面微分幾何的理論。並由他的學生黎曼發展為黎曼幾何。與德國的物理學家韋伯(wilhelm Eduavd Weber，1804—1891)一道建立了電磁學中的高斯單位制; 1833年還和韋伯一起發明瞭電磁電極。高斯的治學態度十分嚴謹。他的格言是 “瑰麗的大廈建成後，應拆除雜亂無章的腳手架。” 因此他發表的每篇著作都是經過仔細推敲、無懈可擊的精品。因此，發表的論文比研究工作要少得多，但研究項目可在日記和書信中見到。全集包括日記、書信共計12捲。他是19世紀前半世紀最偉大的數學家。

取自"https://wiki.mbalib.com/zh-tw/%E9%AB%98%E6%96%AF%E7%A7%AF%E5%88%86"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Tracy,Dan,赵先生,陈cc.

頁面分類: 數學定理

評論(共0條)

提示:評論內容為網友針對條目"高斯積分"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

高斯積分

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是高斯積分

高斯積分的內容

高斯積分通過極限求解

高斯積分與Γ函數的關係

高斯積分的n維和一般化

高斯積分帶線性項的n維

高斯積分提出者人物簡介

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

高斯積分

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是高斯積分

高斯積分的內容

高斯積分通過極限求解

高斯積分與Γ函數的關係

高斯積分的n維和一般化

高斯積分帶線性項的n維

高斯積分提出者人物簡介

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈