模糊理論

出自 MBA智库百科(https://wiki.mbalib.com/)

模糊理論(Fuzzy Logic)

　　概念是思維的基本形式之一，它反映了客觀事物的本質特征。人類在認識過程中，把感覺到的事物的共同特點抽象出來加以概括，這就形成了概念。比如從白雪、白馬、白紙等事物中抽象出“白”的概念。一個概念有它的內涵和外延，內涵是指該概念所反映的事物本質屬性的總和，也就是概念的內容。外延是指一個概念所確指的對象的範圍。例如“人”這個概念的內涵是指能製造工具，並使用工具進行勞動的動物，外延是指古今中外一切的人。

　　所謂模糊概念是指這個概念的外延具有不確定性，或者說它的外延是不清晰的，是模糊的。例如“青年”這個概念，它的內涵我們是清楚的，但是它的外延，即什麼樣的年齡階段內的人是青年，恐怕就很難說情楚，因為在“年輕”和“不年輕”之間沒有一個確定的邊界，這就是一個模糊概念。

　　需要註意的幾點：首先，人們在認識模糊性時，是允許有主觀性的，也就是說每個人對模糊事物的界限不完全一樣，承認一定的主觀性是認識模糊性的一個特點。例如，我們讓100個人說出“年輕人”的年齡範圍，那麼我們將得到100個不同的答案。儘管如此，當我們用模糊統計的方法進行分析時，年輕人的年齡界限分佈又具有一定的規律性；

　　其次，模糊性是精確性的對立面，但不能消極地理解模糊性代表的是落後的生產力，恰恰相反，我們在處理客觀事物時，經常藉助於模糊性。例如，在一個有許多人的房間里，找一位“年老的高個子男人”，這是不難辦到的。這裡所說的“年老”、“高個子”都是模糊概念，然而我們只要將這些模糊概念經過頭腦的分析判斷，很快就可以在人群中找到此人。如果我們要求用電腦查詢，那麼就要把所有人的年齡，身高的具體數據輸入電腦，然後我們才可以從人群中找這樣的人。

　　最後，人們對模糊性的認識往往同隨機性混淆起來，其實它們之間有著根本的區別。隨機性是其本身具有明確的含義，只是由於發生的條件不充分，而使得在條件與事件之間不能出現確定的因果關係，從而事件的出現與否表現出一種不確定性。而事物的模糊性是指我們要處理的事物的概念本身就是模糊的，即一個對象是否符合這個概念難以確定，也就是由於概念外延模糊而帶來的不確定性。

　　模糊理論是在美國加州大學伯克利分校電氣工程系的L.A.zadeh教授於1965年創立的模糊集合理論的數學基礎上發展起來的,主要包括模糊集合理論、模糊邏輯、模糊推理和模糊控制等方面的內容.

　　早在20世紀20年代,著名的哲學家和數學家B.Russell就寫出了有關"含糊性"的論文.他認為所有的自然語言均是模糊的,比如"紅的"和"老的" 等概念沒有明確的內涵和外延,因而是不明確的和模糊的.可是,在特定的環境中,人們用這些概念來描述某個具體對象時卻又能心領神會,很少引起誤解和歧義.

　　美國加州大學的L.A.Zadeh教授在1965年發表了著名的論文，文中首次提出表達事物模糊性的重要概念:隸屬函數,從而突破了19世紀末勒內·笛卡爾（Rene Descartes）的經典集合理論,奠定模糊理論的基礎.

　　1966年,P.N.Marinos發表模糊邏輯的研究報告,1974年,L.A.Zadeh發表模糊推理的研究報告,從此,模糊理論成了一個熱門的課題。

　　1974年,英國的E.H.Mamdani首次用模糊邏輯和模糊推理實現了世界上第一個實驗性的蒸汽機控制,並取得了比傳統的直接數字控制演算法更好的效果,從而宣告模糊控制的誕生。1980年丹麥的L.P.Holmblad和Ostergard在水泥窯爐採用模糊控制並取得了成功,這是第一個商業化的有實際意義的模糊控制器。

　　事實上,模糊理論應用最有效，最廣泛的領域就是模糊控制,模糊控制在各種領域出人意料的解決了傳統控制理論無法解決的或難以解決的問題,並取得了一些令人信服的成效。

　　模糊控制的基本思想:

　　把人類專家對特定的被控對象或過程的控制策略總結成一系列以"IF(條件)THEN(作用)"形式表示的控制規則,通過模糊推理得到控製作用集,作用於被控對象或過程.控製作用集為一組條件語句,狀態語句和控製作用均為一組被量化了的模糊語言集,如"正大","負大","正小","負小",零等。

　　模糊控制的幾個研究方向:

• 模糊控制的穩定性研究
• 模糊模型及辯識
• 模糊最優控制
• 模糊自組織控制
• 模糊自適應控制
• 多模態模糊控制

　　模糊控制的主要缺陷:

　　信息簡單的模糊處理將導致系統的控制精度降低和動態品質變差.若要提高精度則必然增加量化級數,從而導致規則搜索範圍擴大,降低決策速度,甚至不能實時控制. 模糊控制的設計尚缺乏系統性,無法定義控制目標.控制規則的選擇,論域的選擇,模糊集的定義,量化因數的選取多採用試湊發,這對複雜系統的控制是難以奏效的。

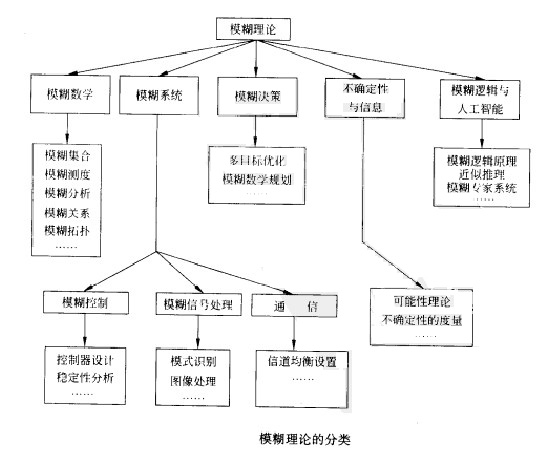
　　模糊理論是指用到了模糊集合的基本概念或連續隸屬度函數的理論。根據下圖可將模糊理論進行大致的分類。主要有五個分支：

　　(1)模糊數學，它用模糊集合取代經典集合從而擴展了經典數學中的概念；

　　(2模糊邏輯與人工智慧，它引入了經典邏輯學中的近似推理，且在模糊信息和近似推理的基礎上開發了專家系統；

　　(3)模糊系統，它包含了信號處理和通信中的模糊控制和模糊方法；

　　(4)不確定性和信息，它用於分析各種不確定性；

　　(5)模糊決策，它用軟約束來考慮優化問題。

　　當然，這五個分支並不是完全獨立的，他們之間有緊密的聯繫。例如，模糊控制就會用到模糊數學和模糊邏輯中的概念。

　　從實際應用的觀點來看，模糊理論的應用大部分集中在模糊系統上，尤其集中在模糊控制上。也有一些模糊專家系統應用於醫療診斷和決策支持。由於模糊理論從理論和實踐的角度看仍然是新生事物，所以我們期望，隨著模糊領域的成熟，將會出現更多可靠的實際應用。

　　模糊理論是以模糊集合(fuzzy set)為基礎，其基本精神是接受模糊性現象存在的事實，而以處理概念模糊不確定的事物為其研究目標，並積極的將其嚴密的量化成電腦可以處理的訊息，不主張用繁雜的數學分析即模型來解決模型。

　　模糊理論發展至今已接近三十餘年，應用的範圍非常廣泛，從工程科技到社會人文科學都可以發現模糊理論研究的蹤跡與成果。我們分別由工程科技與社會人文科學的角度，瞭解模糊理論應用的範疇。

　　一、工程科技方面

　　1、型樣識別：文字識別、指紋識別、手寫字體辨識、影像辨識、語音辨識

　　2、控制工程：機器人控制、汽車控制、家電控制、工業儀錶控制、電力控制

　　3、信號及資訊處理：影像處理、語音處理、資料整理、資料庫管理

　　4、人工智慧及專家系統：故障診斷、自然語言處理、自動翻譯、地震預測、工業設計

　　5、環保：廢水處理、凈水處理廠工程、空氣污染檢驗、空氣品質監控

　　6、其他：建築結構分析、化工製程控制

　　二、 教育、社會及人文科學方面

　　1、教育：教學成果評量、心理測驗、性向測驗、電腦輔助教學

　　2、心理學：心理分析、性向測驗

　　3、決策決定：決策支援、決策分析、多目標評價、綜合評價、險分析