生日攻击
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
什么是生日攻击[1]
生日攻击是指在网络安全中利用生日现象,找到冲突的密码学哈希函数值,伪造报文,攻击报文身份验证算法的模式。
生日攻击的种类[2]
一、签名方案中的生日攻击
艾丽斯要通过某种签名方案对文档的散列值签名来签署一个电子文档,假设散列函数产生一个50比特的输出,她担心佛瑞德(Fred)哄骗她签署另外一个合同,也许是关于佛罗里达的沼泽地。由于欺骗性的合同和正确的文档有相同散列值的概率是1 / 250,这大概是1 / 1015,因此艾丽斯感觉是安全的。佛瑞德可以尝试许多欺骗性的合同,但是他找到有相同散列值的合同的可能性非常小,但是佛瑞德研究了生日问题并且照着下面的方法去做,他找到了能够对文档进行细微改变的30个位置:在一行的末尾增加一个空格,略微改变一个词的拼写,等等。在每一个位置他有两个选择,要么做一个细微的改变要么保留原状,因此他能够产生230个本质上与原始文档相同的文档,同样他得到230个欺骗性的合同并且存储它们的散列值。考虑最初的生日问题,其中r = 230并且n = 250,我们有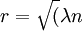 ).其中λ = 210 = 1024。因此一个好文档的版本和一个欺骗性的合同有相同散列值的概率是
).其中λ = 210 = 1024。因此一个好文档的版本和一个欺骗性的合同有相同散列值的概率是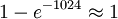 。佛瑞德找到这一对匹配的文档,并且让艾丽斯签署其中好的文档版本,他计划将她的签名附加在欺骗性的合同之上,由于它们有相同的散列值,因此签名对于欺骗性的合同将会有效,所以佛瑞德会声称艾丽斯同意购买沼泽地。然而艾丽斯是一个英语教师,她坚持从一个句子中删除一个逗号,这样就和佛瑞德要求她签名的文档有着完全不同的散列值,佛瑞德又被挫败了,这时他面临的问题是找到一个欺骗性的合同和新的正确文档具有相同的散列值,这根本是不可能的。
。佛瑞德找到这一对匹配的文档,并且让艾丽斯签署其中好的文档版本,他计划将她的签名附加在欺骗性的合同之上,由于它们有相同的散列值,因此签名对于欺骗性的合同将会有效,所以佛瑞德会声称艾丽斯同意购买沼泽地。然而艾丽斯是一个英语教师,她坚持从一个句子中删除一个逗号,这样就和佛瑞德要求她签名的文档有着完全不同的散列值,佛瑞德又被挫败了,这时他面临的问题是找到一个欺骗性的合同和新的正确文档具有相同的散列值,这根本是不可能的。
佛瑞德的行为被称为生日攻击,由于生日攻击有效地将比特数对分,在实际应用中只要你认为有必要,就可以对输出使用两次散列函数。对于签名方案的生日攻击,艾丽斯所做的是一种可取的方法,在签名电子文档时要做一个小的改动。
二、基于离散对数的生日攻击
假设我们处理一个大的素数P,并且想要计算Lα(Β),换句话说,我们想要解αx = Β(modp),通过生日攻击,我们很可能做到。
构造两个列表,长度都大概是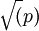 ;
;
1.对于随机选择的近似于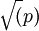 的k值,第一个列表包含数字αk(modp)。
的k值,第一个列表包含数字αk(modp)。
2.对于随机选择的近似于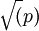 的l值,第二个列表包含数字Βα − 1(modp)。有可能第一个列表的某个元素和第二个列表的某个元素相匹配。如果这样,我们有
的l值,第二个列表包含数字Βα − 1(modp)。有可能第一个列表的某个元素和第二个列表的某个元素相匹配。如果这样,我们有
αk = Β − 1,因此
因此,x = k + 1 + l(modp − 1)是期望的离散对数。
生日攻击的方法解释[3]
下面详细描述生日攻击的方法。
设h:X->Y是一个Hash函数,X和Y都是有限的,并且|X|>=2|Y|,记|X|=m,|Y|=n。显然至少有n个碰撞,问题是如何去找到这些碰撞。一个很自然的方法是随机选择k个不同的元素x1,x2,x3,.....,xk ∈X,计算yI=h(xi),1<=i<=k,然后确定是否有一个碰撞发生。这个过程类似于把k个球随机地扔到n个箱子里边,然后检查看是否某一箱子里边至少有两个球。k个球对应于k个随机数x1,x2,x3,.....,xk,n个箱子对应于Y中的n个可能的元素。我们将计算用这种方法找到一个碰撞的概率的下界,该下界只依赖于k和n,而不依赖于m。
因为我们关心的是碰撞概率的下界,所以可以假定对所有y∈Y,有|h-1(y)|≈m/n。这个假定是合理的,这是因为如果原像集h-1(y)( y∈Y)不是近似相等的,那么找到一个碰撞的概率将增大。
因为原像集h-1(y)( y∈Y)的个数都近似相等,并且xI(1<=i<=k)是随机选择的,所以可将yI=h(xi),1<=i<=k视作Y中的随机元素(yi(1<=i<=k)未必不同)。但计算k个随机元素y1,y2, .....yk∈Y是不同的概率是一件容易的事情。依次考虑y1,y2, .....yk。y1可任意地选择;y2 ≠y1的概率为1-1/n;y3 ≠y1 ,y2的概率为1-2/n;.....;yk ≠y1,y2, .....,yk-1的概率为1-(k-1)/n。
因此,没有碰撞的概率是(1-1/n)(1-2/n).....(1-(k-1)/n)。如果x是一个比较小的实数,那么1-x≈e-x,这个估计可由下式推出:e-x=1-x+x2/2!-x3/3!+ .....。现在估计没有碰撞的概率(1-1/n)(1-2/n).....(1-(k-1)/n)约为1-e-k(k-1)/2n。我们设ε是至少有一个碰撞的概率,则ε≈1-e-k(k-1)/2n,从而有k2-k≈nln(1/(1-ε)2)。去掉-k这一项,我们有k2≈nln(1/(1-ε)2),即k≈sqrt(2nln(1/(1-ε)2))。
如果我们取ε=0.5,那么k≈1.17 sqrt(n)。这表明,仅sqrt(n)个X的随机的元素就能以50%的概率产生一个碰撞。注意ε的不同选择将导致一个不同的常数因子,但k与sqrt(n)仍成正比例。
如果X是一个教室中的所有学生的集合,Y是一个非闰年的365天的集合,h(x)表示学生x的生日,这时n=365,ε=0.5,由k≈1.17 sqrt(n)可知,k≈22.3。因此,此生日问题的答案为23。
生日攻击隐含着消息摘要的长度的一个下界。一个40比特长的消息摘要是很不安全的,因为仅仅用220(大约一百万)次随机Hash可至少以1/2的概率找到一个碰撞。为了抵抗生日攻击,通常建议消息摘要的长度至少应取为128比特,此时生日攻击需要约264次Hash。安全的Hash标准的输出长度选为160比特是出于这种考虑。
中间相遇攻击是生日攻击的一种变形,它不比较Hash值,而是比较链中的中间变量。这种攻击主要适用于攻击具有分组链结构的Hash方案。中间相遇攻击的基本原理为:将消息分成两部分,对伪造消息的第一部分从初试值开始逐步向中间阶段产生r1个变量;对伪造消息的第二部分从Hash结果开始逐步退回中间阶段产生r2个变量。在中间阶段有一个匹配的概率与生日攻击成功的概率一样。
在修正分组攻击中,为了修正Hash结果并获得期望的值,伪造消息和一个分组级联。这种攻击通常应用于最后一个组,因此也称为修正最后分组攻击。差分分析是攻击分组密码的一种方法。这种攻击也可用来攻击某些Hash算法。
针对Hash算法的一些弱点可对Hash算法进行攻击,可利用Hash算法的代数结构及其所使用的分组密码的弱点来攻击一些Hash方案。例如针对DES的一些弱点(即互补性、弱密钥、密钥碰撞等)来攻击基于DES的Hash方案。








This explanation is not as clear as the one on Wiki