辛普森悖论
出自 MBA智库百科(https://wiki.mbalib.com/)
辛普森悖论(Simpson's Paradox)又译为辛普森诡论
目录 |
辛普森悖论(Simpson's Paradox)亦有人译为辛普森诡论,为英国统计学家E.H.辛普森(E.H.Simpson)于1951年提出的悖论,即在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论。
例一:一所美国高校的两个学院,分别是法学院和商学院,新学期招生。人们怀疑这两个学院有性别歧视。现作如下统计:
法学院
| 性别 | 录取 | 拒收 | 总数 | 录取比例 |
|---|---|---|---|---|
| 男生 | 8 | 45 | 53 | 15.1% |
| 女生 | 51 | 101 | 152 | 33.6% |
| 合计 | 59 | 146 | 205 |
商学院
| 性别 | 录取 | 拒收 | 总数 | 录取比例 |
|---|---|---|---|---|
| 男生 | 201 | 50 | 251 | 80.1% |
| 女生 | 92 | 9 | 101 | 91.1% |
| 合计 | 293 | 59 | 352 |
根据上面两个表格来看,女生在两个学院都被优先录取。即女生的录取比率较高。现在将两学院的数据汇总:
| 性别 | 录取 | 拒收 | 总数 | 录取比例 |
|---|---|---|---|---|
| 男生 | 209 | 95 | 304 | 68.8% |
| 女生 | 143 | 110 | 253 | 56.5% |
| 合计 | 352 | 205 | 557 |
在总评中,女生的录取比率反而比男生低。
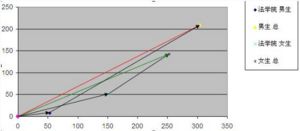
借助一幅向量图可以更好的了解情况(右图)这个例子说明,简单的将分组数据相加汇总,是不能反映真实情况的。
就上述例子说,导致辛普森悖论有两个前提。
1、两个分组的录取率相差很大,就是说法学院录取率很低,而商学院却很高。而同时两种性别的申请者分布比重相反。女性申请者的大部分分布在法学院,相反,男性申请者大部分分布于商学院。结果在数量上来说,拒收率高的法学院拒收了很多的女生,男生虽然有更高的拒收率,但被拒收的 数量却相对不算多。而录取率很高的商学院虽然有较高的录取比例,但是被拒收的男生数量相对法学院来说则明显较多。
2、有潜在因素影响着录取情况。就是说,性别并非是录取率高低的唯一因素,甚至可能是毫无影响的。至于在学院中出现的比率差,可能是随机事件。又或者是其他因素作用,比如入学成绩,却刚好出现这种录取比例,使人牵强误认为这是由性别差异而造成的。
辛普森悖论的回避[1]
为了避免辛普森悖论出现,就需要斟酌个别分组的权重,以一定的系数去消除以分组资料基数差异所造成的影响,同时必需了解该情境是否存在其他潜在要因而综合考虑。
辛普森悖论的管理[1]
辛普森悖论就像是欲打100场篮球比赛,然后以总胜率评价好坏,于是有人专找高手挑战20场而胜1场,另外80场找平手挑战而胜40场,结果胜率41%,另一人则专挑高手挑战80场而胜8场,而剩下20场平手打个全胜,结果胜率为28%,比41%小很多,但仔细观察挑战对象,后者明显较有实力。
量与质是不等价的,无奈的是量比质来得容易量测,所以人们总是习惯用量来评定好坏,而此数据却不是重要的。除了质与量的迷思之外,辛普森悖论的另外一个启示是:如果我们在人生的抉择上选择了一条比较难走的路,就得要有可能不被赏识的领悟,所以这算是怀才不遇这个成语在统计上的诠释!
评论(共23条)
分组数据汇总时该同化分母:比如纯%数据。没有统一标准的数据是不该统计在一起的--因为结论与论据不在同一个坐标系。饽论只是因果穿越喏坐标系--要没有矛盾:需要翻译坐标系。
莴感觉莴有点晕~瞎say
看到这个让我想到中国的人均住房面积等一系列的人均数据。
有同感
看到这个让我想到中国的人均住房面积等一系列的人均数据。
我的第一感觉也是中国相关部门的人均面积、人均收入!
因为一个素不相识的人换了个大房子,和自己毛线关系没有,而据相关部门统计说我人均住房面积增加了,我的生活水平提高了,啊,举国同庆!
人家工资涨了1千,我的不变,又据相关部门统计说我人均收入增加了,我的生活水平提高了,啊,举国同庆!
问一下为什么斜率可以表示录取率啊?希望你们还在 时隔7年
看到这个让我想到中国的人均住房面积等一系列的人均数据。
平均数的误差在于其容易受极值影响,跟辛普森悖论没关系。






加权啊加权