多先验期望效用模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
决策分析的很大一部分工作都是关于不确定性问题的决策研究。Savage的主观期望效用模型由于其简单灵活,已成为分析人类不确定情况下决策行为的最重要理论。但是,由于现实世界太复杂,人们肘具有不确定性的决策对象可能没有比较全面的了解,因此不能用单个主观概率分布来描述不确定事件,当然也就不能用主观期望效用模型来解决这类问题。鉴于此,人们还提出了其他一些模型,如Wald准则,乐观准则,Hurwitz准则及Laplace准则等。但是,这些准则中,Laptave准则是主观期望效用模型的特例,其他准则都有走向另一极端的嫌疑,决策者几乎对具有不确定性的决策对象不作任何限制,与现实的决策情形不太相容,直接用于不确定性的决策是令人怀疑的。
Savage的主观期望效用理论并非无懈可击,其公理化假定看起来是合乎情理的,但在实际决策中是有问题的。著名的Ellsberg悖论表明:当面对不确定情况下的决策时,大多数人表现出对不确定性的厌恶,称之为不确定性厌恶,或模糊性厌恶。针对这种现象,人们对Savage的公理体系进行了一些改造,主要有Sehmeidler提出的Choquet期望效用模型及Gilboa和Schmeidler提出的多先验期望效用模型。多先验期望效用模型不要求唯一主观概率分布,也并非对不确定事件不作任何限制,是目前国外应用比较广逆的、较好的不确定性决策理论之一。
关于Gilboa和Sehmeidler的多先验期望效用模型是为了刻划Ellsberg悖论所描述的不确定性厌恶现象而提出的。先给出以下记号:
任意拓扑空间Y,M(Y)表示关于Y的概率测度集;
X:输出空间;
S:自然状态集,任意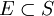 ,称为事件;
,称为事件;
Fs={f,有界,可测f:S→M(X)},是决策人的可行行动集,若对任意s ∈S,f(s)=P∈M(X)称是f常行动,常行动集记为F;
任意f,g∈F,a∈[0,1],记h=af+(1-a)g,对任意s∈S,有h(s)=af(s)+ (1-a)g(s)
记》为定义在F上的二元偏好关系。在此基础上定义偏好无差异关系“~”为,f~g,其中f,g∈F,若f》g,且g》f,定义严格偏好关系为“>”,f>g,若f》g,但f~g不成立。
在上述记号的假定下,定义以下公理:
公理1:(弱序)
(i)(完全性)任意f,g∈F,要么f》g,要么g》f;
(ii)(传递性)任意f,g,h∈F,若f》g,g》h,则f》h;
公理2:(连续性)
任意f,g,h∈F,若f> g,g> h,则存在α,β∈(0,1),使得αf + (1 − α)h > g > βf + (1 − β)h
公理3:(确定性独立)
任意f,g∈ F,且h∈P,对任意a∈(0,1),f> g当且仅当af+(1-a)h>ag+(1-a)h
此独立性假定其对常行动有效。
公理4:(单调性)
任意f,g∈F,若任意s∈S,f(s)》g(s),则,f》g
公理5:(不确定性厌恶)
任意f,g∈F,a∈(O,1),f~g,则af+(1-a)g》f
公理5不排除af+(1-ag)>f的可能性,即有不确定性厌恶的向。
公理6:(非退化性)
存在f,g∈F,f>g
Gilboa-Schmeidler定理: 下述条件等价
(i)F上的排序》满足公理1—5
(ii)存在线性函数u:M(X)→R,和非空闭凸集C,它是关于S的有限可加概率测度集合,使得任意f,g∈F
f》g当且仅当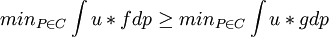 (1)
(1)
此外,(a)函数u在正线性变换下唯一;(b)F上的排序》满足公理1— 6,则C唯一。
此定理说明:具有不确定性厌恶惯向的决策者可用多先验概率分布族C表示不确定因素,而在求救用时取在C上的最小值。其思想是:当面对不确定性时,决策者用多先验概率描述它。C是决策者对不确定性的信念;仅当决策者具有不确定性厌恶倾向时,取在C上的最小效用,再求最大化此救用的行动。如果决策者不是不确定性厌恶的,则没有必要也不能取在c上的最小效用,决策依据不再是(1)式。
多先验期望效用模型中的行动是从状态到后果分布的函数,一个状态可能有几个不同的后果,对应的是一个关于后果集的抽奖。这里直接简化为,对同一行动,状态和后果是一一对应的,f:S→X。同时,后果用效用表示
一般地,不确定性决策问题可由三元组表示{S,F,u),其中
S = (s1,...,sm),为有限状态集;
F = (f1,...,fn),为有限行动集;
u = (uij)n * m,状态为Sj时行动fi的后果,即效用。
对多先验期望效用模型,引入概率测度集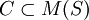 ,不确定性决策问题可表示为四元组{S,F,u,C)。由Gilboa—Schmeidler定理,优化目标是求f'∈F,使得
,不确定性决策问题可表示为四元组{S,F,u,C)。由Gilboa—Schmeidler定理,优化目标是求f'∈F,使得
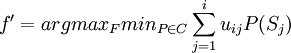
1. Wald准则
取C=M(S),即所有可能分布,有
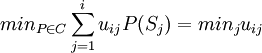
从而
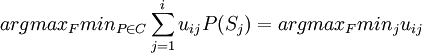
与Wald准则完全一样
由此看来,可将多先验期望效用模型看成是Wald准则的理论基础。C=M(S)表示决策者对不确定事件的认识是平凡的,什么情况都可能出现。Wald准则是绝对不砖定性厌恶决策者的决策准则。
2.Laplace准则
取C={P∈M(S)|P(Sj)=1/m,j=1,⋯ ,m),多先验期望效用模型就转化为Laplace准则。在这种情况下,决策者认为不确定事件状态是等可能出现的。从多先验期望效用模型的观点看,没有考虑决策者没有考虑不确定性厌恶情况。从Savage的主观期望效用模型的观点看,决策者的主观概率是不确定事件状态是等可能的。
应该注意,即使C含多个概率分布,若决策者是不确定性中立的(指依然使用期望妓用来作为评价标准),则总存在概率分布P’∈M(S),使得以此作为Savage的主观概率,用主观期望效用模型得到的解与不确定性中立时的解一致。事实上,不妨设q是C上的概率分布,注意C是闭凸的,E(·)为数学期望,有
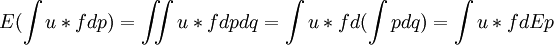
取P'= Ep即可。
从上面的讨论可以看出,Wald准则和Laplace准则均为多先验期望效用模型的特殊情形。一个是绝对不确定性厌恶决策者的准则,一个是不确定性中立决策者的准则。虽然大量试验表明,大多数决策者表现出Ellsberg悖论所描述的情形,但也有一些例外;同时,多先验期望效用模型最主要的思想是可将自然状态的不确定性表示为具有多个概率分布的集合。对不确定性的态度不仅仅只有厌恶和中立,还有其他种类,比如不确定性追求;另外,厌恶程度和追求程度的大小也有区别,我们大可用其他形式体现。
3. 乐观准则
乐观准则是求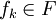 ,使得fk = argmaximaxjuij
,使得fk = argmaximaxjuij
取C=M(s),有 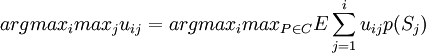
如果说Wald准则是绝对不确定性厌恶决策者的具体表现,那么,乐观准则完全是绝对不确定性厌恶决策者的决策准则。将C缩小在较小的范围内,乐观准则即为在一定范围内的乐观。这样,这一准则可能更受欢迎,因为在不确定性中可能存在部分确定性。毕竟,人们对大多数不确定性不会一无所知
4. Hurwitz准则
Hurwitz准则是指选择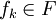 ,使得fk = argmaxi(1 − λ)minjuij + λmaxjuij
,使得fk = argmaxi(1 − λ)minjuij + λmaxjuij
其中![\lambda \in[0,1]](/w/images/math/a/d/a/ada29722c713d4d8a571d9a4ce353ae6.png) ,称为乐观系数。
,称为乐观系数。
取C=M(S),上式可写为
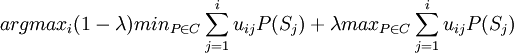
与3类似,不必要求C= M(S),完全可将不确定事件中的某些确定性在信念C中表现出来,有助于决策的选择。乐观系数在C的范围内起作用。我们甚至可以对上式两个不同部分采用不同的C,可行的解释是悲观时的信念与乐观时的信念不一致。





