多先驗期望效用模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
決策分析的很大一部分工作都是關於不確定性問題的決策研究。Savage的主觀期望效用模型由於其簡單靈活,已成為分析人類不確定情況下決策行為的最重要理論。但是,由於現實世界太複雜,人們肘具有不確定性的決策對象可能沒有比較全面的瞭解,因此不能用單個主觀概率分佈來描述不確定事件,當然也就不能用主觀期望效用模型來解決這類問題。鑒於此,人們還提出了其他一些模型,如Wald準則,樂觀準則,Hurwitz準則及Laplace準則等。但是,這些準則中,Laptave準則是主觀期望效用模型的特例,其他準則都有走向另一極端的嫌疑,決策者幾乎對具有不確定性的決策對象不作任何限制,與現實的決策情形不太相容,直接用於不確定性的決策是令人懷疑的。
Savage的主觀期望效用理論並非無懈可擊,其公理化假定看起來是合乎情理的,但在實際決策中是有問題的。著名的Ellsberg悖論表明:當面對不確定情況下的決策時,大多數人表現出對不確定性的厭惡,稱之為不確定性厭惡,或模糊性厭惡。針對這種現象,人們對Savage的公理體系進行了一些改造,主要有Sehmeidler提出的Choquet期望效用模型及Gilboa和Schmeidler提出的多先驗期望效用模型。多先驗期望效用模型不要求唯一主觀概率分佈,也並非對不確定事件不作任何限制,是目前國外應用比較廣逆的、較好的不確定性決策理論之一。
關於Gilboa和Sehmeidler的多先驗期望效用模型是為了刻劃Ellsberg悖論所描述的不確定性厭惡現象而提出的。先給出以下記號:
任意拓撲空間Y,M(Y)表示關於Y的概率測度集;
X:輸出空間;
S:自然狀態集,任意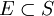 ,稱為事件;
,稱為事件;
Fs={f,有界,可測f:S→M(X)},是決策人的可行行動集,若對任意s ∈S,f(s)=P∈M(X)稱是f常行動,常行動集記為F;
任意f,g∈F,a∈[0,1],記h=af+(1-a)g,對任意s∈S,有h(s)=af(s)+ (1-a)g(s)
記》為定義在F上的二元偏好關係。在此基礎上定義偏好無差異關係“~”為,f~g,其中f,g∈F,若f》g,且g》f,定義嚴格偏好關係為“>”,f>g,若f》g,但f~g不成立。
在上述記號的假定下,定義以下公理:
公理1:(弱序)
(i)(完全性)任意f,g∈F,要麼f》g,要麼g》f;
(ii)(傳遞性)任意f,g,h∈F,若f》g,g》h,則f》h;
公理2:(連續性)
任意f,g,h∈F,若f> g,g> h,則存在α,β∈(0,1),使得αf + (1 − α)h > g > βf + (1 − β)h
公理3:(確定性獨立)
任意f,g∈ F,且h∈P,對任意a∈(0,1),f> g當且僅當af+(1-a)h>ag+(1-a)h
此獨立性假定其對常行動有效。
公理4:(單調性)
任意f,g∈F,若任意s∈S,f(s)》g(s),則,f》g
公理5:(不確定性厭惡)
任意f,g∈F,a∈(O,1),f~g,則af+(1-a)g》f
公理5不排除af+(1-ag)>f的可能性,即有不確定性厭惡的向。
公理6:(非退化性)
存在f,g∈F,f>g
Gilboa-Schmeidler定理: 下述條件等價
(i)F上的排序》滿足公理1—5
(ii)存線上性函數u:M(X)→R,和非空閉凸集C,它是關於S的有限可加概率測度集合,使得任意f,g∈F
f》g當且僅當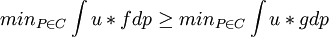 (1)
(1)
此外,(a)函數u在正線性變換下唯一;(b)F上的排序》滿足公理1— 6,則C唯一。
此定理說明:具有不確定性厭惡慣向的決策者可用多先驗概率分佈族C表示不確定因素,而在求救用時取在C上的最小值。其思想是:當面對不確定性時,決策者用多先驗概率描述它。C是決策者對不確定性的信念;僅當決策者具有不確定性厭惡傾向時,取在C上的最小效用,再求最大化此救用的行動。如果決策者不是不確定性厭惡的,則沒有必要也不能取在c上的最小效用,決策依據不再是(1)式。
多先驗期望效用模型中的行動是從狀態到後果分佈的函數,一個狀態可能有幾個不同的後果,對應的是一個關於後果集的抽獎。這裡直接簡化為,對同一行動,狀態和後果是一一對應的,f:S→X。同時,後果用效用表示
一般地,不確定性決策問題可由三元組表示{S,F,u),其中
S = (s1,...,sm),為有限狀態集;
F = (f1,...,fn),為有限行動集;
u = (uij)n * m,狀態為Sj時行動fi的後果,即效用。
對多先驗期望效用模型,引入概率測度集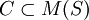 ,不確定性決策問題可表示為四元組{S,F,u,C)。由Gilboa—Schmeidler定理,優化目標是求f'∈F,使得
,不確定性決策問題可表示為四元組{S,F,u,C)。由Gilboa—Schmeidler定理,優化目標是求f'∈F,使得
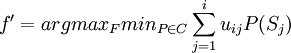
1. Wald準則
取C=M(S),即所有可能分佈,有
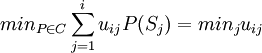
從而
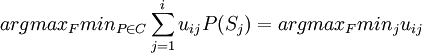
與Wald準則完全一樣
由此看來,可將多先驗期望效用模型看成是Wald準則的理論基礎。C=M(S)表示決策者對不確定事件的認識是平凡的,什麼情況都可能出現。Wald準則是絕對不磚定性厭惡決策者的決策準則。
2.Laplace準則
取C={P∈M(S)|P(Sj)=1/m,j=1,⋯ ,m),多先驗期望效用模型就轉化為Laplace準則。在這種情況下,決策者認為不確定事件狀態是等可能出現的。從多先驗期望效用模型的觀點看,沒有考慮決策者沒有考慮不確定性厭惡情況。從Savage的主觀期望效用模型的觀點看,決策者的主觀概率是不確定事件狀態是等可能的。
應該註意,即使C含多個概率分佈,若決策者是不確定性中立的(指依然使用期望妓用來作為評價標準),則總存在概率分佈P’∈M(S),使得以此作為Savage的主觀概率,用主觀期望效用模型得到的解與不確定性中立時的解一致。事實上,不妨設q是C上的概率分佈,註意C是閉凸的,E(·)為數學期望,有
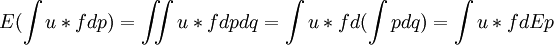
取P'= Ep即可。
從上面的討論可以看出,Wald準則和Laplace準則均為多先驗期望效用模型的特殊情形。一個是絕對不確定性厭惡決策者的準則,一個是不確定性中立決策者的準則。雖然大量試驗表明,大多數決策者表現出Ellsberg悖論所描述的情形,但也有一些例外;同時,多先驗期望效用模型最主要的思想是可將自然狀態的不確定性表示為具有多個概率分佈的集合。對不確定性的態度不僅僅只有厭惡和中立,還有其他種類,比如不確定性追求;另外,厭惡程度和追求程度的大小也有區別,我們大可用其他形式體現。
3. 樂觀準則
樂觀準則是求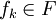 ,使得fk = argmaximaxjuij
,使得fk = argmaximaxjuij
取C=M(s),有 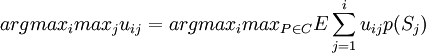
如果說Wald準則是絕對不確定性厭惡決策者的具體表現,那麼,樂觀準則完全是絕對不確定性厭惡決策者的決策準則。將C縮小在較小的範圍內,樂觀準則即為在一定範圍內的樂觀。這樣,這一准則可能更受歡迎,因為在不確定性中可能存在部分確定性。畢竟,人們對大多數不確定性不會一無所知
4. Hurwitz準則
Hurwitz準則是指選擇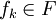 ,使得fk = argmaxi(1 − λ)minjuij + λmaxjuij
,使得fk = argmaxi(1 − λ)minjuij + λmaxjuij
其中![\lambda \in[0,1]](/w/images/math/a/d/a/ada29722c713d4d8a571d9a4ce353ae6.png) ,稱為樂觀繫數。
,稱為樂觀繫數。
取C=M(S),上式可寫為
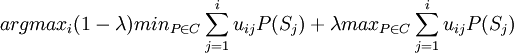
與3類似,不必要求C= M(S),完全可將不確定事件中的某些確定性在信念C中表現出來,有助於決策的選擇。樂觀繫數在C的範圍內起作用。我們甚至可以對上式兩個不同部分採用不同的C,可行的解釋是悲觀時的信念與樂觀時的信念不一致。





