纯粹生存保险

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

(重定向自纯粹的生存保险)

什么是纯粹生存保险

　　纯粹生存保险也叫做n年纯生存保险，是指被保险人在保险合同签订的时间期满存活，将得到合同规定的保险金。即现龄x岁的人在投保n年后仍然存活，可以在第n年末获得生存赔付的保险。

[编辑]

纯粹生存保险的精算现值

　　假设(x)投纯粹的生存保险，保期为n年，如果n年后仍存活，将得到1单位元的保险金，求这一保险在投保时的现值。

　　(1) ${}_n\!E_x$ 表示这一现值

　　(2)设x岁时，有 $l x$ 人购买了这种保险，于是在 $(x + n)$ 岁时，将有 $l (x + n)$ 人存活。

　　则有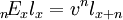： ${}_n\!E_x l_x=v^n l_{x+n}$

　　即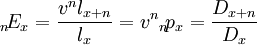： ${}_n\!E_x=\frac{v^n l_{x+n}}{l_x}=v^n{}_n\!p_x=\frac{D_{x+n}}{D_x}$

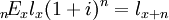
　　(3) ${}_n\!E_x l_x (1+i)^n=l_{x+n}$

　　现实意义的解释：

　　 ${}_n\!E_x$ ：在利率和生者利下n年的折现系数；

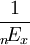　　 $\frac{1}{{}_n\!E_x}$ :在利率和生者利下n年的累计系数。

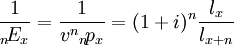　　 $\frac{1}{{}_n\!E_x}=\frac{1}{v^n {}_n\!p_x}=(1+i)^n\frac{l_x}{l_{x+n}}$ ，

　　它是利率累积因子 $(1 + i) n$ 与生存累积因子 $\frac{l_x}{l_{x+n}}$ 的乘积。

来自"https://wiki.mbalib.com/wiki/%E7%BA%AF%E7%B2%B9%E7%94%9F%E5%AD%98%E4%BF%9D%E9%99%A9"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

y桑.

页面分类: 保险术语

评论(共0条)

提示:评论内容为网友针对条目"纯粹生存保险"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

纯粹生存保险

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是纯粹生存保险

纯粹生存保险的精算现值

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

查看

工具箱▼

纯粹生存保险

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是纯粹生存保险

纯粹生存保险的精算现值

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈