民间定理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　民间定理是指任给一个有限n人博弈G的协调期望赢得向量U,都存在一个足够接近于1的概率值，使得每个局中人计算未来赢得的概率都大于该值时，U成为G的无限次重复博弈的某个纳什均衡的每一轮的期望赢得向量。

　　设原博弈的一次性博弈有均衡得益数组优于ω，那么在该博弈的多次重复中，所有不小于个体理性得益的可实现得益，都至少有一个子博弈完美纳什均衡来实现它们。

　　其目的：对各博弈方至少可实现的得益，和最佳情况下可实现的得益等进行考虑，以确定能实现得益的分布范围。

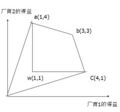
　　由点a,b,c所构成的两条连线（包括三个点）代表了帕累托效率意义上的最有效率的均衡得益。

　　设G是一个完全信息的静态博弈。用(e1,…,en)记G的纳什均衡得益，用(x1,…, xn)表示G的任意可实现得益，如果xi>ei对于任意博弈方i都成立，而δ足够接近1，那么无限次重复博弈G(∞,δ)中一定存在一个子博弈完美纳什均衡，各博弈方的平均得益就是(x1,…, xn)。

　　民间定理正是在于保证了这些得益可以由一定次数重复博弈的子博弈完美纳什均衡的平均得益来实现或逼近它们。