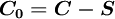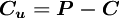期望损失最小法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　期望损失最小法是指比较不同订货量下的期望损失，取期望损失最小的订货量作为最佳订货量。^[1]

　　期望损失＝超储损失之和+缺货损失之和

　　已知库存物品的单位成本为C，单位售价为P，若在预定的时间内卖不出去，则单价只能降为S(S<C)卖出，单位超储损失为C_o = C − S；若需求超过存货，则单位缺货损失(机会损失)C_u = P − C。设订货量为Q时的期望损失为E_l(Q)，则取使EL(Q)最小的Q作为最佳订货量。E_l(Q)可通过下式计算：

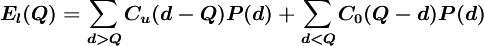
　　其中:

• 单位超储损失
• 单位缺货损失
• P:单价;Q:订货量;d:需求量;C;单位成本;P(d):需求量为d时的概率;s:预订时间卖不出去的售价;

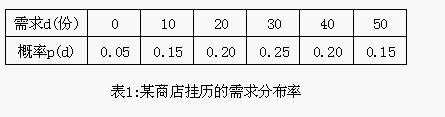
　　按过去的记录，新年期间对某商店挂历的需求分布率如表1所示:

　　已知：每份挂历的进价为C＝50元，售价P＝80元。若在1个月内卖不出去，则每份挂历只能按S＝30元卖出。求：该商店应该进多少挂历为好。

　　解:设该商店买进Q份挂历当实际需求d<Q 时，将有一部分挂历卖不出去，每份超储损失为Co=C-S=50-30=20（元）；

• 当实际需求d > Q 时，将有机会损失，每份欠储损失为Cu=P-C=80-50=30（元）。
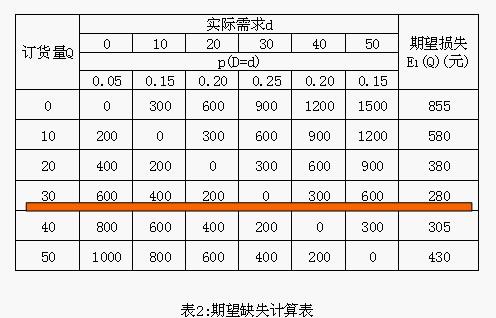
• 当Q=30时，则E_l(Q)=[30×(40-30)×0.20+30×(50-30)×0.15]+[20×(30-0)×0.05+20×(30-10)×0.15+20×(30-20)×0.20]=280（元）。
• 当Q取其它值时，可按同样方法算出EL(Q)，结果如表2所示,由表2可以得出最佳订货量为30份。