里昂惕夫生产函数
出自 MBA智库百科(https://wiki.mbalib.com/)
里昂惕夫生产函数又称固定投入比例生产函数,是指在每一个产量水平上任何一对要素投入量之间的比例都是固定的生产函数。假定生产过程中只使用劳动和资本两种要素,则固定投入比例生产函数的通常形式为:
Q = Min(L/U,K/V)
其中,Q表示一种产品的产量,L和K分别表示劳动和资本的投入量,U和V分别表示为固定的劳动和资本的生产技术系数,它们分别表示生产一单位产品所需要的固定的劳动投入量和资本投入量。该生产函数表示产量Q取决于两个比值L/U和K/V中较小的那一个,即使其中的一个比例数值较大,也不会提高产量。在这里,Q的生产被假定为必须按照L和K之间的固定比例,当一种生产要素的数量不能变动时,另一种生产要素的数量再多,也不能增加产量。需要指出的是,在该生产函数中,一般通常假定生产要素投入量L,K都满足最小的要素投入组合的要求,所以有:
Q = L/U =K/V 即 K/L =V/U
上式清楚地体现了该生产函数的固定投入比例的性质,在这里,它等于两种要素的固定的生产技术系数之比。对于一个固定投入比例生产函数来说,当产量发生变化时,各要素的投入量以相同的比例发生变化,所以,各要素的投入量之间的比例维持不变。关于固定投入比例生产函数的这一性质,可以用几何图形来说明。
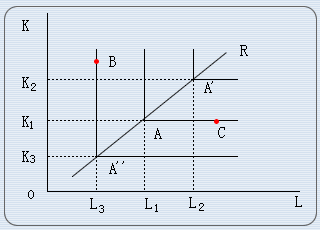
如上图,横轴和纵轴分别表示劳动和资本的投入数量,分别以A,A1和A2为顶点的三条含有直角的实线,顺次表示生产既定的产量Q1、Q2和Q3的各种要素组合。以生产Q1的产量来说,A的要素组合(K1,L1)是生产产量Q1的最小的要素投入量组合。以A点为顶点的两条直角边上的任何一点(不包括A点),都不是生产Q1产量的最小的要素投入组合,例如,B点表示资本投入量过多,C点表示劳动投入量过多。如果产量由Q1增加为Q2,或由Q减少为Q3,则最小要素投入组合相应地会由A点移至A1点,或由A点移至A2点。此时,两要素投入量以相同的比例增减,两要素投入比例保持不变,即:
K1/L1=K2/L2=K3/L3=V/U
因此,从原点出发经过A2、A和A1点的射线OR表示了这一固定比例生产函数的所有产量水平的最小要素投入量的组合。








V,U是要素价格之比吗