无广告阅读 
免验证复制 
微信支付 
支付宝 
PayPal 一次指数平滑法
出自 MBA智库百科(https://wiki.mbalib.com/)
一次指数平滑法(Single exponential smoothing)
目录[隐藏] |
一次指数平滑法是指以最后的一个第一次指数平滑。如果为了使指数平滑值敏感地反映最新观察值的变化，应取较大阿尔法值，如果所求指数平滑值是用来代表该时间序列的长期趋势值，则应取较小阿尔法值。同时，对于市场预测来说，还应根据中长期趋势变动和季节性变动情况的不同而取不同的阿尔法值，一般来说，应按以下情况处理：
1.如果观察值的长期趋势变动接近稳定的常数，应取居中阿尔法值(一般取0.6—0.4)使观察值在指数平滑中具有大小接近的权数；
2.如果观察值呈现明显的季节性变动时，则宜取较大的阿尔法值(一般取0.6一0.9)，使近期观察在指数平滑值中具有较大作用，从而使近期观察值能迅速反映在未来的预测值中；
3.如果观察值的长期趋势变动较缓慢，则宜取较小的e值(一般取0.1—0.4)，使远期观察值的特征也能反映在指数平滑值中。在确定预测值时，还应加以修正，在指数平滑值S，的基础上再加一个趋势值b，因而，原来指数平滑公式也应加一个b。
一次指数平滑法是根据前期的实测数和预测数，以加权因子为权数，进行加权平均，来预测未来时间趋势的方法。
一次指数平滑法计算公式为：
yt + 1 = axt + (1 − a)yt
式中， xt―― 时期 t 的实测值；
yt―― 时期 t 的预测值；
a―― 平滑系数，又称加权因子，取值范围为0≤a≤1。
将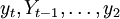
的表达式逐次代入yt + 1中，展开整理后，得：
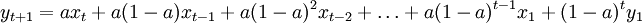
从上式中可以看出，一次指数平滑法实际上是以a(1 − a)k为权数的加权移动平均法。由于k越大，a(1 − a)k越小，所以越是远期的实测值对未来时期平滑值的影响就越小。 在展开式中，最后一项y1为初始平滑值，在通常情况下可用最初几个实测值的平均值来代替，或直接可用第 1 时期的实测值来代替。
从上式可以看出，新预测值是根据预测误差对原预测值进行修正得到的。a的大小表明了修正的幅度。a值愈大，修正的幅度愈大，a值愈小，修正的幅度愈小。 因此，a值既代表了预测模型对时间序列数据变化的反应速度，又体现了预测模型修匀误差的能力。
在实际应用中，a值是根据时间序列的变化特性来选取的。 若时间序列的波动不大，比较平稳，则a应取小一些，如0.1 ～ 0.3 ；若时间序列具有迅速且明显的变动倾向， 则a应取大一些，如 0.6 ～ 0.9 。实质上，aa是一个经验数据，通过多个值进行试算比较而定，哪个a值引起的预测误差小，就采用哪个。
1、取第一期的实际值为初值；
2、取最初几期的平均值为初值。
一次指数平滑法比较简单，但也有问题。问题之一便是力图找到最佳的α值，以使均方差最小，这需要通过反复试验确定。
评论(共2条)
//Swift version func forecastS1(input x:[Double],weight a:Double)->Double{ var count = Double(x.count)
return x[0..<x.count].reduce(0.0){ defer{ count -= 1 } return $0 + $1 * a * pow(1-a, count-1) } + pow(1-a, Double(x.count)) * x[0] }
simple exponential smoothing is the time serious method most frequently used for demand forecasting . it also smooth out the blips in the data ,but it's power over the n period is three fold , 1) old data never dropped 2. old data are given progressively lees weight , 3. the caculation is simple and only require the most recent data.