纳什均衡
出自 MBA智库百科(https://wiki.mbalib.com/)
纳什均衡(Nash equilibrium)——完全信息静态博弈
目录 |
纳什均衡,又称为非合作博弈均衡,是博弈论的一个重要术语,以约翰·纳什命名。在一个博弈过程中,无论对方的策略选择如何,当事人一方都会选择某个确定的策略,则该策略被称作支配性策略。如果两个博弈的当事人的策略组合分别构成各自的支配性策略,那么这个组合就被定义为纳什均衡。
一个策略组合被称为纳什均衡,当每个博弈者的均衡策略都是为了达到自己期望收益的最大值,与此同时,其他所有博弈者也遵循这样的策略。
关于纳什均衡的普遍意义和存在性定理的证明等奠定非合作博弈理论发展基础的重要成果,是约翰·纳什在普林斯顿大学攻读博士学位时完成的。实际上,博弈论的研究起始于1944年冯·诺依曼(Von Neumann)和奥斯卡·摩根斯坦(Oscar Morgenstern)合著的《博弈论和经济行为》。然而却是纳什首先用严密的数学语言和简明的文字准确地定义了纳什均衡这个概念,并在包含“混合策略(mixed strategies)”的情况下,证明了纳什均衡在n人有限博弈中的普遍存在性,从而开创了与诺依曼和摩根斯坦框架路线均完全不同的“非合作博弈(Non-cooperative Game)”理论,进而对“合作博弈(Cooperative Game)”和“非合作博弈”做了明确的区分和定义。阿尔伯特·塔克(Albert tucker)教授评价其论文,“这是对博弈理论的高度原创性和重要的贡献。它发展了本身很有意义的n人有限非合作博弈的概念和性质。并且它很可能开拓出许多在两人零和问题以外的,至今尚未涉及的问题。在概念和方法两方面,该论文都是作者的独立创造。”
1.囚徒困境
博弈论中一个著名的例子就是囚徒困境。囚徒困境是一个非零和博弈,说的是两个嫌疑犯甲和乙私入民宅联手作案,被警方逮住但未获证据。警方于是将两个嫌疑犯分开审讯。警官分别告诉 两个囚犯,如果你招供,而对方不招供,则你将被判刑3个月,对方将被判刑10年;若两人都不招供则因未获证据但私入民宅将各拘留1年;如果两人均招供,每人将被判刑5年。于是,两个人同时陷入招供还是不招供的两难处境。结果是,尽管甲不知乙是否招供,但他认为自己选择“招供”最好,因而甲会选择“招供”,同样乙也会选择“招供”,两人各判5年。而两人都选择不招供,虽证据不足但因私入民宅将各拘留1年的结果是不会出现的。
| 博弈矩阵 | 囚犯甲 | ||
|---|---|---|---|
| 招供 | 不招供 | ||
| 囚犯乙 | 招供 | 判刑五年 | 甲判刑十年;乙判刑三个月 |
| 不招供 | 甲判刑三个月;乙判刑十年 | 判刑一年 | |
在一个博弈过程中,无论对方的策略选择如何,当事人一方都会选择某个确定的策略,则该策略被称作支配性策略。如果两个博弈的当事人的策略组合分别构成各自的支配性策略,那么这个组合就被定义为纳什均衡。纳什均衡又称为非合作博弈均衡,是博弈论的一个重要术语,它是以美国数学家、日后成为电影《美丽心灵》主人公的纳什的名字命名的。在上述囚徒困境例子中,两个囚犯符合自己利益的选择是坦白招供。这种两人都选择坦白的策略以及因此被判刑五年的结局就是“纳什均衡”。
2.打猎
两个猎人出发去打猎。假设一头鹿有400公斤肉,但必须两人合作才能打到,一个人打什么都获得不了。同地区有一群兔子,一共有200公斤肉,两人合作可以全部打完,但一个人打也可以获得100公斤肉。两个猎人各自都知道对方的平衡策略,但不能通过任何方式影响对方的决策。最终的结果会怎样?
| 决策 | 结果 | ||
|---|---|---|---|
| A | B | A | B |
| 猎鹿 | 猎鹿 | 200 | 200 |
| 猎鹿 | 猎兔 | 0 | 100 |
| 猎兔 | 猎鹿 | 100 | 0 |
| 猎兔 | 猎兔 | 100 | 100 |
这里面有两个纳什均衡。
(1)两人都猎鹿:任何一人单方切换成猎兔子,都会让自己的收益从200跌到100。
(2)两人都猎兔子:任何一人单方切换成猎鹿,都会让自己的收益从100跌到0。
注意,这里面都是单方更改。要是双方同时从兔子换成鹿,都会更好——但纳什均衡不考虑这个。
这也造成了一个问题:纳什均衡从全局看起来不见得是“理性”的,不是看起来的最优解,但是对每个人来说,它的确是在别人不可控时自己的最优解。
纳什均衡的重要影响[1]
纳什均衡理论奠定了现代主流博弈理论和经济理论的根本基础,正如克瑞普斯(Kreps,1990)在《博弈论和经济建模》一书的引言中所说,“在过去的一二十年内,经济学在方法论以及语言、概念等方面,经历了一场温和的革命,非合作博弈理论已经成为范式的中心……在经济学或者与经济学原理相关的金融、会计、营销和政治科学等学科中,现在人们已经很难找到不懂纳什均衡能够‘消费’近期文献的领域。”纳什均衡的重要影响可以概括为以下六个方面(谢识予,1999):
(1)改变了经济学的体系和结构。非合作博弈论的概念、内容、模型和分析工具等,均已渗透到微观经济学、宏观经济学、劳动经济学、国际经济学、环境经济学等经济学科的绝大部分学科领域,改变了这些学科领域的内容和结构,成为这些学科领域的基本研究范式和理论分析工具,从而改变了原有经济学理论体系中各分支学科的内涵。
(2)扩展了经济学研究经济问题的范围。原有经济学缺乏将不确定性因素、变动环境因素以及经济个体之间的交互作用模式化的有效办法,因而不能进行微观层次经济问题的解剖分析。纳什均衡及相关模型分析方法,包括扩展型博弈法、逆推归纳法、子博弈完美纳什均衡等概念方法,为经济学家们提供了深入的分析工具。
(3)加强了经济学研究的深度。纳什均衡理论不回避经济个体之间直接的交互作用,不满足于对经济个体之间复杂经济关系的简单化处理,分析问题时不只停留在宏观层面上而是深入分析表象背后深层次的原因和规律,强调从微观个体行为规律的角度发现问题的根源,因而可以更深刻准确地理解和解释经济问题。
(4)形成了基于经典博弈的研究范式体系。即可以将各种问题或经济关系,按照经典博弈的类型或特征进行分类,并根据相应的经典博弈的分析方法和模型进行研究,将一个领域所取得的经验方便地移植到另一个领域。
(5)扩大和加强了经济学与其他社会科学、自然科学的联系。纳什均衡之所以伟大,就因为它普通,而且普通到几乎无处不在。纳什均衡理论既适用于人类的行为规律,也适合于人类以外的其他生物的生存、运动和发展的规律。纳什均衡和博弈论的桥梁作用,使经济学与其他社会科学、自然科学的联系更加紧密,形成了经济学与其他学科相互促进的良性循环。
(6)改变了经济学的语言和表达方法。在进化博弈论方面相当有造诣的坎多利(Kandori,1997)对保罗·萨缪尔森(Paul Samuelson)的名言“你甚至可以使一只鹦鹉变成一个训练有素的经济学家,因为它必须学习的只有两个词,那就是‘供给’和‘需求’”,曾做过一个幽默的引申,他说,“现在这只鹦鹉需要再学两个词,那就是‘纳什均衡’”。
案例一:纳什均衡在货币政策效应中的应用[2]
- 一、博弈论下的货币政策博弈分析
货币政策博弈分析 利用博弈论方法分析宏观金融博弈问题。因而,博弈论是宏观金融博弈分析的方法论基础。纳什(Nash) 在195O年和1951年发表了两篇关于非合作博弈的重要文章,从一般意义上定义了非合作博弈及其均衡解.并证明了均衡的存在.基本奠定了现代非合作博弈论的基础。因而,该均衡以后被博弈理论称为“纳什均衡”。即是指由所有的参与者的最优策略组成的策略组合。在这种策略组合中 给定其他参与者的策略,没有任何单个参与者有积极性选择其他策略 也就没有人主动去打破这种均衡。相反如果一种均衡或制度安排,如果不是一种纳什均衡.即不是所有参与者的最优策略组合 那么,这种组合就不能成立或者至少不能持续。合作博弈强调团体理性、效率和公平。而非合作博弈强调个人理性、个人最优决策。其结果可能是有效的 也可能是无效的。现实中 大量的经济博弈问题是非合作博弈。非合作博弈理论的发展为其在经济研究中的广泛应用创造了条件并推动了合作博弈的进一步发展。
纳什均衡假定博弈参与者在选择自己的策略时,把其他参与者的策略当做给定的。而不考虑自己的选择如何影响博弈对手的选择。这个假定在静态博弈下是成立的,但在动态博弈下却不成立。
在静态博弈中,所有参与者同时行动,不可能在自己采取行动前观察到其他人的行动 因而就无暇反应。但在动态博弈中 一方行动在先 另一方行动在后.后者自然会根据前者的选择而调整自己的选择,前者自然会理性地预期到这一点,所以不能不考虑自己的选择对其他参与者的影响,由于决策者不考虑自己的选择对他人选择的影响,纳什均衡允许了不可置信威胁的存在。1965年泽尔腾(Selten) 将纳什均衡的概念引入了动态分析定义了子博弈精练纳什均衡” 的概念。将不可置信的威胁策略从纳什均衡中剔除出去,从而解决了完全信息动态博弈均衡求解问题 将不可置信的策略变成可置信策略的行动 即经济学中的 承诺行动”。如果当事人不履行其承诺时将为之付出相应的代价 这种承诺就是可置信的,否则就是不可置信的。该概念的提出,对利用博弈论方法研究货币政策问题奠定了基础。
- 二、纳什均衡在货币政策效应中的应用
在理性预期条件下,我们考察一期的货币政策博弈均衡。假定中央银行的目标成本函数为: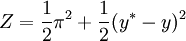 。
。
其中:π为通货膨胀率;y为实际经济增长率;y * 为中央银行期望的经济增长率。
根据卢卡斯供给曲线:y = yn + α(π − πe),α > 0.其中: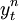 为潜在经济增长率;
为潜在经济增长率;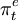 为公众的预期通货膨胀率:a表示非预期通膨胀对经济的影响程度,即总供给曲线的斜率。
为公众的预期通货膨胀率:a表示非预期通膨胀对经济的影响程度,即总供给曲线的斜率。
假定α=1,即:y = yn + (π − πα)
同时假定中央银行对货币增长有完全的控制能力.公众的预期完全理性 不存在真实供给冲击和货币流通速度变化的影响.通货膨胀率π等于货币供给增长率m,通货膨胀预期πα。等于货币供给增长率me,中央银行期望的经济增长率与潜在的经济增长率相等。有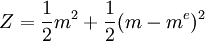 。
。
令公众的目标函数为避免由于预期误差导致的通货膨胀之害,因此可把公众的效用函数定义为:U = − (m − me)2
可得该货币政策博弈的支付矩阵如下:
| 中央银行策略(m) | 公众策略(me) | |
| 0 | 1 | |
| 0 | (0,0) | (0,0,5) |
| 1 | (1,-1) | (0,5,0) |
矩阵中m=0表示中央银行选择零的货币增长率 m=1表示中央银行选择正的货币增长率:公众策略的含义同上。由支付矩阵可知 对中央银行来说,m=1的效用严格优于m=0的效用.m=1为其最优策略。在理性预期下,公众迅速认识到中央银行会选择正的货币增长率,其必然选择m=1以使其效用最大化,该博弈模型的纳什均衡是中央银行选择正的货币增长率,公众选择正的通货膨胀率预期,效用函数为(0,5,0)。均衡结果显示货币政策只会影响通货膨胀率而真实产出不变。
货币政策博弈具体表现为货币政策的决策和执行过程中存在动态不一致性问题。博弈主体在当前做出的关于未来的最优决策,在决策执行时对决策制定者已不再是最优决策.因而他必然要调整其决策。例如 在公众预期形成之前 对于货币政策制定者来说,零通货膨胀(或较低通货膨胀)可能是最优的选择。因而为了影响公众预期,他可能在此选择和许诺他将实行零通货膨胀(或较低通货膨胀)。但是,当公众预期形成以后零通货膨胀(或较低通货膨胀)对政策制定者来说已不是最优决策。为了获得非预期通货膨胀对经济增长和就业增加的刺激作用,政策制定者必须实行正的(或更高的)通货膨胀.在完全信息条件下公众知道政策制定者会这样做.因而他的许诺是不可置信的。具有理性和完全信息的公众不会被其愚弄.最后结果必然是被预期到的正的(或更高的)通货膨胀。相机选择货币政策的这种通货膨胀(通货紧缩)倾向是由该博弈结构内生性决定的,即该均衡(纳什均衡)允许了不可置信的威胁策略的存在,中央银行关于零通胀(或低通胀)的许诺是不可置信的。
要消除货币政策的通货膨胀(通货紧缩)倾向 必须消除这种不可置信因素——中央银行在公众预期形成之前承诺其将毫不改变地执行单一规则的货币政策 通过承诺行动中央银行获得了影响公众预期的能力。因而,在选择其货币供给增长率时.就必须考虑它对公众预期的立即和充分的影响 就不能期望制造非预期通货膨胀(通货紧缩)来刺激经济、增加就业或为预算融资。这就是说,提高政策的稳定性和可信程度是消除通货膨胀(通货紧缩)的关键。
本条目由以下用户参与贡献
Vulture,Angle Roh,山林,Mingshi,苦行者,Zfj3000,Leonardolee,Yixi,laogaogao,Dan,郭凯,金龙,Mis铭,赵丽娜,otf125,M id 6cbe1c39db3914adbbd5c9437b981725,LuyinT.评论(共68条)
越是多数人觉得容易理解的理论或道理,越是难以用简陋的文字和图表表示清楚.所以,能解释简单道理的人,往往都疯掉了,原因最简单的就是只有一个人疯了,对大部分琐碎都麻木了,他才能有足够的时间,精力和注意力去接近和感受真相.
越是多数人觉得容易理解的理论或道理,越是难以用简陋的文字和图表表示清楚.所以,能解释简单道理的人,往往都疯掉了,原因最简单的就是只有一个人疯了,对大部分琐碎都麻木了,他才能有足够的时间,精力和注意力去接近和感受真相.
你在講什麼東西?還是先把中文讀好再來寫評論吧!
NASH的理论最烦的不是2个囚徒和坦白,抵赖的运算。是N个囚徒和N种方式的概率实现,那就烦了。 只有2种当然容易理解,但有N行乘N列的MATRIX运算,那头就大喽。。。
纳什精神出现状况并不因为这“简单的理论”,而是因为对数字超乎寻常的敏感~ 甚至用公式来计算很多随机性的事件 可以这样说吧 说不定他还能通过算法分析计算出你在闹市捡到100块之后的行为
你们有没想过 如果这2个人重复进行多次博弈 而且多人多次进行这样的博弈 最后会这么样呢 你们能得到答案吗 能解出多人多次这样博弈如果你想获得最后的成功 你要用什么样的策略呢
有没有人能够告诉我 占优策略是否就一定是纳什均衡呢?
不管其他人选择什么策略,最优选择都是某一个固定的策略,也就是“以不变应万变”。那么这个固定的策略就是占优策略。如果每个参与人都有占优策略,那么这些占优策略的组合就是占优均衡。比如囚徒困境中,“招供”就是每个参与人的占优策略,(招供,招供)就是占优均衡。
纳什均衡也是各参与人策略的组合。它的要求没有占优均衡这么强,它只要求在这个组合中,给定其他人的选择,这个选择是最优的,而不要求“不管其他人怎么选择,我的这个选择都是最优的”。
说白了就是:占优均衡是一种特殊的纳什均衡。
囚徒困境不是纳什均衡,是占优均衡。请不要误传。
个人觉得,条目中的囚徒困境例子,只是想表达在囚徒困境中存在着纳什均衡
例子那里有点问题.大家发现了吗.
应该是: 1,两个人都不招,那么只按盗窃罪,两个人同时最多只判一年. 2,第二方面,甲/乙招了,而对方刚好没招,那么招认一方轻判3个月,对方(不招一方)将被重判10年 3,双方都招了,一起判5年
例子那里没说清楚前提,也说错了服刑的时间.
个人觉得这个例子是有问题的。如果是你,你会招供么?显然不会,你也不会担心你的同伙会招供。因为如果他招供的话他要做一年牢,如果他不招供的话只会做三个月,同理你也是。互相不担心对方会招供,谁还会招供。所以我觉得作者应该把他招你不招改成他服刑三个月你服刑10年,都不招供改成服刑1年。
发现了,看的时候就觉得有问题。发表了评论才发现你已经提出来了。
有没有看过电影《美丽心灵》 一个讲述约翰纳什的美丽故事 不仅为他的数学才能折服
看过,很感人~真的被约翰纳什震撼了
这个说法是正道。
为什么这么间单的理论会搞到人疯掉
他不是搞這個理論然後瘋了 納什自己說對數字圖形等非常的敏感使他產生了幻覺 The idea I had about supernatural beings came to me the same way that my mathematical ideas did. So I took them seriously.----A Beautiful Mind.
覺得簡單是因為在我們之前雙贏的理論就已經被提出了,如果沒有人提出的情況下你想到并證明了,像納什這樣,那你也是一個開拓者。
听到NASH 这个名字一股热情涌上来了,神秘的均衡~~ 翻译的作者也无法理解NASH Equilibrium,所以他写的是自己能理解的部分加工翻译的吧。 也不要怪他,他也没办法.应该谢谢. 那位知道中文版 NASH Equilibrium 详细的书? 请推荐.
原文已修正,谢谢指正哦~并添加了新的案例,希望对您有帮助哦~
有没有看过电影《美丽心灵》 一个讲述约翰纳什的美丽故事 不仅为他的数学才能折服
我就是看了之后,才初次了解纳什均衡,一段时间内疯狂的爱数学!超赞的电影!!!!!!!!!!!
有没有看过电影《美丽心灵》 一个讲述约翰纳什的美丽故事 不仅为他的数学才能折服
超赞的电影!!
囚徒困境不是纳什均衡,是占优均衡。请不要误传。
囚徒困境就是典型的纳什博弈,我现在正在学习纳什博弈,囚徒困境时教科书中举出的例子。不懂请别装懂。
有谁能告诉我这四种的关系么? 1.Static Nash equilibrium 2.Prisoner’s dilemma and Battle of the sexes 3.Cournot and Bertrand Duopoly 4.Mixed Strategy 好像是说后面三种是第一种的example?是这样么?
为什么这么间单的理论会搞到人疯掉
这是个平凡而又伟大的理论,平凡因为普通,伟大是因为可以说这么复杂。
为什么这么间单的理论会搞到人疯掉
那就问问自己为什么1+1=2有人论证了几十年
这个理论厉害在把复杂的写的很简单, 并把这个理论用数字给表达出来了。 说简单的估计你看不懂那个公式吧。 不要轻看任何被大部分世界科学家都赞同的理论。
数学不好的就别逼逼了,你能看得懂例子不代表这个理论简单。人家只是用一个通俗的例子来说明一个数学问题,说到底,这还是个数学问题。
囚徒困境不是纳什均衡,是占优均衡。请不要误传。
占优均衡就是强纳什均衡
越是多数人觉得容易理解的理论或道理,越是难以用简陋的文字和图表表示清楚.所以,能解释简单道理的人,往往都疯掉了,原因最简单的就是只有一个人疯了,对大部分琐碎都麻木了,他才能有足够的时间,精力和注意力去接近和感受真相.
越简单越不容易用平常的眼光去看待
为什么这么间单的理论会搞到人疯掉
简单源于无知
为什么这么间单的理论会搞到人疯掉
读读纳什的博士论文,可能疯掉都搞不懂。或者买本梯若尔的教材、博弈论文集再了解一下。
你在講什麼東西?還是先把中文讀好再來寫評論吧!
你写的是什么东西?还是先把汉语和中文都学好再来评论吧!
你在講什麼東西?還是先把中文讀好再來寫評論吧!
你写的什么东西,学好中文再来评论吧,这么简单的一句话都读不懂,还指责别人
为什么这么间单的理论会搞到人疯掉
你看美丽心灵电影就知道了,纳什精神状况出现问题不是因为这个理论,而是当时的时代背景。






为什么这么间单的理论会搞到人疯掉