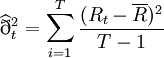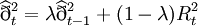变异数-共变异数法
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
(重定向自相关法)
目录 |
[编辑]
变异数-共变异数法也称为相关法(Correlation Method),参数(Parametric)法、线型(Linear)法或一阶常态(Delta-Normal)法 。
主要的假设就是个别资产报酬率符合联合常态分配,而且具有序列独立的特性。
由这些资产所构成的线性组合资产,一定会服从常态分配,藉由常态分配的性质再来估计出给定评估期间与信赖机率水平下的风险值。
常态分配的假设使得变异数-共变异数法可以快速的算出风险值。
[编辑]
纳入个别资产间的相关性,进而建构整个投资组合于未来评估期间的损益(或报酬)分配。
[编辑]
传统上通常利用移动平均的观念来估算变异数,并且可进一步分为等权移动平均与指数加权移动平均两种方式。
相等(简单)加权移动平均法
指数加权移动平均法