数学模型
出自 MBA智库百科(https://wiki.mbalib.com/)
数学模型(Mathematical Model)
目录 |
数学模型是针对参照某种事物系统的特征或数量依存关系,采用数学语言,概括地或近似地表述出的一种数学结构,这种数学结构是借助于数学符号刻画出来的某种系统的纯关系结构。从广义理解,数学模型包括数学中的各种概念,各种公式和各种理论。因为它们都是由现实世界的原型抽象出来的,从这意义上讲,整个数学也可以说是一门关于数学模型的科学。从狭义理解,数学模型只指那些反映了特定问题或特定的具体事物系统的数学关系结构,这个意义上也可理解为联系一个系统中各变量间内的关系的数学表达。
数学模型所表达的内容可以是定量的,也可以是定性的,但必须以定量的方式体现出来。因此,数学模型法的操作方式偏向于定量形式。
建立数学模型的要求:
1、真实完整。
1)真实的、系统的、完整的反映客观现象;
2)必须具有代表性;
3)具有外推性,即能得到原型客体的信息,在模型的研究实验时,能得到关于原型客体的原因;
4)必须反映完成基本任务所达到的各种业绩,而且要与实际情况相符合。
2、简明实用。在建模过程中,要把本质的东西及其关系反映进去,把非本质的、对反映客观真实程度影响不大的东西去掉,使模型在保证一定精确度的条件下,尽可能的简单和可操作,数据易于采集。
3、适应变化。随着有关条件的变化和人们认识的发展,通过相关变量及参数的调整,能很好的适应新情况。
1、 精确型:内涵和外延非常分明,可以用精确数学表达。
2、 模糊型:内涵和外延不是很清晰,要用模糊数学来描述。
1、简化原则
现实世界的原型都是具有多因素、多变量、多层次的比较复杂的系统,对原型进行一定的简化即抓住主要矛盾,数学模型应比原型简化,数学模型自身也应是“最简单”的。
2、可推导原则
由数学模型的研究可以推导出一些确定的结果,如果建立的数学模型在数学上是不可推导的,得不到确定的可以应用于原型的结果,这个数学模型就是无意义的。
3、反映性原则
数学模型实际上是人对现实世界的一种反映形式,因此数学模型和现实世界的原型就应有一定的“相似性”,抓住与原型相似的数学表达式或数学理论就是建立数学模型的关键性技巧。
1、解决对客观现象进行试验的困难。
2、比较容易操作。
3、模型试验能够比较节约。
4、可以揭示客观对象本质。
1、提出问题并用准确的语言加以表述。
2、分析各种因素,作出理论假设。
3、建立数学模型。
4、按数学模型进行数学推导,得出有意义的数学结果。
5、对数学结论进行分析。若符合要求,可以将数学模型进行一般化和体系化按此解决问题若不符合,则进一步探讨,修改假设,重建模型,直止符合要求为止。
6、优化。对一个问题的假设和数学模型不断加以修改,进行最优化处理。因为对一个问题或一类问题也可能有几个模型,以对它们要进行比较,直到找到最优模型。
数学模型案例分析[1]
- 1.转库流向优化及时间推荐
转库流向优化及时间推荐和业务需求的提出转库决策主要是从末端库涨库的角度考虑转库问题,是完成推荐转库准发的功能。一个准发是否最终实现转库,取决于末端库、成品库、准发数量、品种的情况和限制。准发因其品种的不同可以转向的成品库有差异,从具体成品库的角度看,在能力不能满足所有准发转库需求的情况下,必须在准发集合中作出取舍;类似的情形也适用于末端库。这就是转库流向优化及时间推荐模型建立的原因。首先,用户希望尽多准发转向最合适的目的库,也就是尽可能的转库。其次,对于某些准发(具体就是合同总重量大于1000吨并上一条船的准发),希望其尽可能的均匀转库。比如有一个2000吨的合同(其中包括10个准发),此合同可以转向5个成品库,那么目标就是转向每个成品库的准发总重都是400吨。一般情况下,由于准发是不可拆分的,此目标不能严格达到,那么就希望总重尽量接近400吨。受客观因素的限制,准发转库的完成要受三类约束条件的限制,第一类是要满足末端库出库能力的约束;第二类是成品库库容的约束;第三类是成品库入库能力的约束。由于末端库和成品库均不是一个,每类实际上都是多个约束。
- 2.转库原则
对于每个待转库的准发,它可转向的库之间有一个优先顺序,此顺序确定的原则如下:。
末端库向成品库转,末端库间不转;。
优先转向厂内成品库。
铁路库的存放原则如下:
A.跨放钢管;
B.跨优先放钢管,可放管坯,大方坯,方坯;
C.跨主要放钢卷,也可以放钢坯,钢板;
D.跨主要放钢板,也可以放板坯、方坯、钢卷;
E,F跨放冷热板卷(主要存放出口产品);
A,B跨可以混用,但不能于其它跨混用;
C,D,E,F跨可以混用。
运输方式已定情况:
厂内铁运全放铁路库;钢坯优先放铁路库,可放堆放场,钢坏堆场;
水运:冷轧产品优先放码头库,可放铁路库;热轧产品国外优先铁路库,其次放码头库,也可放堆场,国内堆场优先;。
钢坯全放堆场;钢管放铁路库;
当多个准发进行转库竞争时,必须需要确定准发的优先级别。具体原则如下:
(1)分品种转库原则:冷轧产品:优先往码头库转,其次往铁路库转,不能露天存放;热轧产品:出口热轧卷、钢坯优先放堆场,然后考虑往铁路库转,热轧板(出口、国内)放铁路库D跨,国内热轧卷,对于水运产品,放码头库;对于铁运产品,放铁路库C跨,其次放堆场,钢坏原则上放堆场,钢管全放铁路库。
(2)汽运、涨库的转库原则同水运。
(3)优先顺序的确定原则:优先考虑当日15点至次日15点的车船合同,优先顺序为直装、涨库、其它:准发单不能拆,优先考虑大的准发单;在制品转库按成品对待,优先顺序按(3)中的“其它”项对待;
- 3.数学模型描述
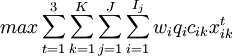 (1)
(1)
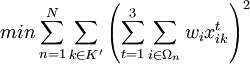 (2)
(2)
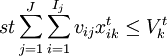 ,t = 1,2,3;
,t = 1,2,3;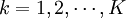 (3)
(3)
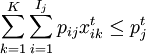 ,t = 1,2,3;
,t = 1,2,3;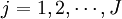 (4)
(4)
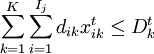 ,t = 1,2,3;
,t = 1,2,3;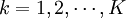 (5)
(5)
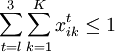 ,
,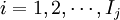 ;
;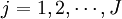 (6)
(6)
各参数的意义如下:
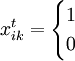
| 第i个准发在第t班转向k库 |
其他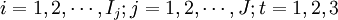
|
j:需转库准发所涉及的末端库,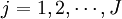 ;
;
Ij:j库需转库的准发集合,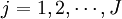 ;
;
k:转库所涉及的成品库,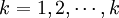 ;
;
cik:i准发转至k库之“收益”;
wi:i准发的重量(吨);
qi:i准发的权重系数;
n:总数量大于等于103吨并同上一条船的合同(或属同一出品联络单)数量,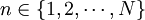 ;
;
K':总数量大于等于103吨并同上一条船的合同(或属同一出口联络单)可能转向的成品库集合;
Ωn:第n个总数量大于等于103吨并同上一条船的合同(或属同一出口联络单)包含的准发的个数;
vik:i准发转向k库时占用的k库库容;
Vtk:k库在第t班的剩余库容;
Pij:j库i准发出库所需能力(件数);
Pjt:j库在第t班转库可用的出库能力(件数);
dik:i准发转至k库所需的入库能力(件数);
Dtk:k库在第t班转库可用的入库能力(单位为件数)。
- 4.解法思想简介及结果
从上面的模型描述中可以看出,这个问题是一个线性整数规划问题,(且为二次0-1规划,同时也是多目标模型)。从解决问题的角度看,当准发数目少时,问题为小规模0-1规划问题,使用线性规划(LP)模块可以解决,而当准发多时问题为大规模0—1规划问题,运行LP模块的花费时间已不能满足实际问题的要求,因为其复杂性已属于指数增长的问题。所以调用现成的程序在其时效上已经是不可行的,这类问题被称NP—完全问题。
在本问题中主要采用两种算法:一种为启发式算法(贪婪算法),另一种为混合算法(线性规划和启发式相结合的算法)。
这个模型有两个目标,目标一的对象是合同重小于一千吨的准发,而目标二的对象为合同重大于等于一千吨的准发,两种准发共享仓库的能力。多目标问题是一类难于求解的问题,解决这一类问题的方法主要有目标加权法、目标规划等。考虑到流向优化及时间推荐模型的一些特殊性,本项目采用的是简单但是合理的一种解法。实际问题是合同重于一千吨的准发数量少,合同不重于一千吨的准发是大量的,分散转库的要求不但重要而且易于满足。因此工程中采用的是两种准发分别处理的方法,即首先处理重于一千吨的准发,能力允许时再转不重于一千吨的准发,这相当于目标加权法中给第一个目标很大的权值。
这种方法不能推广到更一般问题,使用这种方法完全是由于问题的特殊性决定。这样处理后,两个目标可以分开处理,归入第一个目标的准发数量小,使用启发式算法求解;属于第二个目标的准发数量巨大,使用线性规划加启发式算法的方法求解。
单独考虑目标一的问题在数学上可概括为二次0-1规划,它是N个式子每两个之差的平方和最小,要求它们之间的差距最小,故可称为平衡问题。
当变量为实数时,这N个式子的值全相等时目标值最小,但对于0-1变量则一般不会出现这种情况。
从约束来看,这些约束都是小于等于约束,因此是一个典型的资源约束问题。有N个库(成品库)要接受一批准发,在满足三种能力的条件下,希望转到每个库中的准发总重一样大,而且这些准发都是尽量要转库的(转比不转好)。根据以上问题的特点,可以把追求每个式子都等于一个定值作为目标。因此把准发总重用N平均,并把这个值(以后称做期望值)作为每个库希望接受准发总重的目标,这和原问题是等价的。因此,就可以对于每个库分别确定转向它的准发集合,使此准发集合的总重尽量接近期望值,这样当所有的目标库转向的准发均确定后,总的结果就是每个库转向的准发总重是一样的。剩下的问题就是对于一个具体的目标库(成品库)和一个期望转入的准发总重,如何找出转向它的准发集合。本文使用的方法就是上面说的启发式算法,具体的算法由两个算法框图SglRdy和AtMost给出(略)。其中SglRdy的作用就是从可选准发集合中选择重量大于等于期望值的准发进行转库(因为一旦有这样的准发存在,只转一个准发就够了),如果有的话就返回,否则调用AtMost。AtMost的作用就是力求选取总重小于等于期望值的准发集合,使它们的总重尽量接近期望值。这是一种不回溯的搜索算法。
- ↑ 高天 王志福 刘晓刚.大型企业库存管理中的数学模型——转库流向优化及时间推荐.锦州师范学院学报(自然科学版).2000年02期








相当有深度!!