双线性插值

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

双线性插值(Bilinear interpolation)

什么是双线性插值

　　双线性插值又称为双线性内插.在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

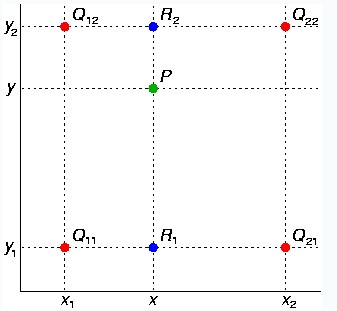
　　红色的数据点与待插值得到的绿色点假如我们想得到未知函数f在点P=(x,y)的值，假设我们已知函数f在 $Q 11 = (x 1, y 1)$ 、 $Q 12 = (x 1 . y 2), Q 21 = (x 2, y 1)$ 以及 $Q 22 = (x 2, y 2)$ 四个点的值。

　　首先在x方向进行线性插值，得到

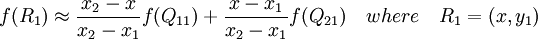
　　 $f(R_1)\approx\frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})\quad where\quad R_1=(x,y_1)$

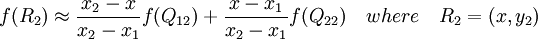
　　 $f(R_2)\approx\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})\quad where\quad R_2=(x,y_2)$

　　然后在y方向进行线性插值，得到

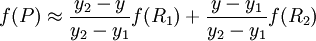
　　 $f(P)\approx\frac{y_2-y}{y_2-y_1}f(R_1)+\frac{y-y_1}{y_2-y_1}f(R_2)$

　　这样就得到所要的结果f(x,y)，

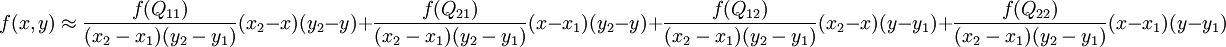
　　 $f(x,y)\approx\frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y_2-y)+\frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y_2-y)+\frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y-y_1)+\frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y-y_1)$

　　如果选择一个坐标系统使得f的四个已知点坐标分别为(0,0)、(0,1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为

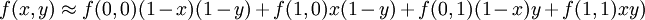
　　 $f(x,y)\approx f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy)$

　　或者用矩阵运算表示为

　　 $f(x,y)\approx\left[1-x\quad x\right]\begin{bmatrix}f(0,0)&f(0,1)\\f(1,0)&f(1,1)\end{bmatrix}\begin{bmatrix}1-y\\y\end{bmatrix}$

　　与这种插值方法名称不同的是，这种插值方法并不是线性的，它的形式是

　　 $(a 1 x + a 2)(a 3 y + a 4)$

　　它是两个线性函数的乘积。另外，插值也可以表示为

　　 $b 1 + b 2 x + b 3 y + b 4 x y$

　　在这两种情况下，常数的数目]都对应于给定的f的数据点数目。

　　线性插值的结果与插值的顺序无关。首先进行y方向的插值，然后进行x方向的插值，所得到的结果是一样的。

　　双线性插值的一个显然的三维空间延伸是三线性插值。

[编辑]

本条目由以下用户参与贡献

Yixi.

页面分类: 应用数学

评论(共2条)

提示:评论内容为网友针对条目"双线性插值"展开的讨论，与本站观点立场无关。

123.235.4.* 在 2011年1月18日 16:49 发表

这里面是不是有错误呀。

回复评论

Yixi (Talk | 贡献) 在 2011年1月19日 11:50 发表

123.235.4.* 在 2011年1月18日 16:49 发表

这里面是不是有错误呀。

感谢您的指正，原文已修正。

回复评论

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

双线性插值

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是双线性插值

相关条目

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共2条)

导航

意见反馈

查看

工具箱▼

双线性插值

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是双线性插值

相关条目

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共2条)

导航

意见反馈