汇率换算：

美元(USD)

美元(USD)
加元(CAD)
日元(JPY)
英镑(GBP)
欧元(EUR)
澳元(AUD)
新台币(TWD)
港元(HKD)
新加坡(SGD)
菲律宾(PHP)
泰铢(THB)

按当月汇率换算，

包含手续费

二次曲线法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

(重定向自二次曲线预测法)

什么是二次曲线法

　　二次曲线法是研究时间序列观察值数据随时间变动呈现一种由高到低再到高(或由低到高再到低)的趋势变化的曲线外推预测方法.由于时间序列观察值的散点图呈现抛物线形状,故也称之为二次抛物线预测模型。

　　假设曲线趋势外推预测模型为：

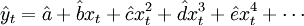
　　 $\hat y_t=\hat a+\hat b x_t+\hat c x_t^2+\hat dx_t^3+\hat e x_t^4+\cdots$

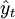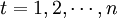　　式中： $\hat y_t$ 第t期某变量的预测值（因变量）； $x t$ ——时间变量（自变量）， $t=1,2,\cdots,n$ 。

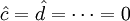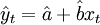　　1) 当 $\hat c=\hat d=\cdots=0$ 时， $\hat y_t=\hat a +\hat b x_t$ ，即为线性趋势外推预测法的模型；

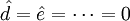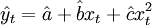　　2) 当 $\hat d=\hat e=\cdots=0$ 时， $\hat y_t=\hat a +\hat b x_t+\hat c x_t^2$ ,即为二次曲线外推预测法的模型。

[编辑]

二次曲线法的计算^[1]

　　用最小二乘法确定待定参数

　　1) 参数的确定

　　设 $y t$ 表示第t期的时间序列的观察值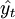； $\hat{y_t}$ ——第t期的预测值； $e t$ ——第t期的离差；Q——离差平方和。由二次曲线外推预测法的模型 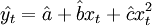$\hat{y_t}=\hat a+\hat bx_t +\hat cx_t ^2$ ，有

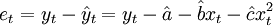
　　 $e_t=y_t-\hat y_t=y_t-\hat a-\hat bx_t-\hat cx_t^2$

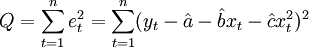　　 $Q=\sum_{t=1}^{n}e_t^2=\sum_{t=1}^{n}(y_t-\hat a-\hat bx_t-\hat cx_t^2)^2$ (3.2.2)

　　与拟合直线外推法相同的原理，对式（3.2.2）求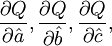 $\frac{\partial Q}{\partial\hat a},\frac{\partial Q}{\partial\hat b},\frac{\partial Q}{\partial\hat c},$ 并分别令其等于0，则可得关于 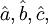$\hat a,\hat b,\hat c,$ 的方程组

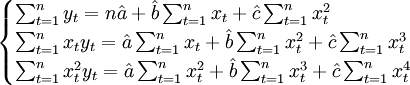　　 $\begin{cases}\sum_{t=1}^n y_t=n\hat a+\hat b\sum_{t=1}^n x_t+\hat c \sum_{t=1}^n x_t^2 \\ \sum_{t=1}^n x_t y_t=\hat a\sum_{t=1}^n x_t+\hat b\sum_{t=1}^n x_t^2+\hat c \sum_{t=1}^n x_t^3 \\ \sum_{t=1}^n x_t^2 y_t=\hat a\sum_{t=1}^n x_t^2+\hat b\sum_{t=1}^n x_t^3+\hat c \sum_{t=1}^n x_t^4 \end{cases}$ (3.2.3)

　　由于 $x t$ 表示时间序列的编号，如同拟合直线方程法一样，当时间序列观察期的项数为奇数时，令其中间项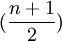 $(\frac{n+1}{2})$ 的编号为0，则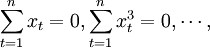 $\sum_{t=1}^n x_t=0,\sum_{t=1}^n x_t^3=0,\cdots,$

　　式(3.2.3)可简化为：

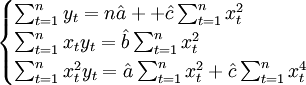　　 $\begin{cases} \sum_{t=1}^n y_t=n\hat a++\hat c \sum_{t=1}^n x_t^2 \\ \sum_{t=1}^n x_t y_t=\hat b\sum_{t=1}^n x_t^2 \\ \sum_{t=1}^n x_t^2 y_t=\hat a\sum_{t=1}^n x_t^2+\hat c \sum_{t=1}^n x_t^4 \end{cases}$ (3.2.4)

　　解上面的方程组可得：

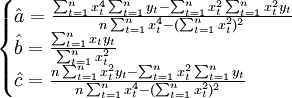　　 $\begin{cases} \hat a=\frac{\sum_{t=1}^n x_t^4 \sum_{t=1}^n y_t-\sum_{t=1}^n x_t^2\sum_{t=1}^n x_t^2y_t}{n\sum_{t=1}^n x_t^4-(\sum_{t=1}^n x_t^2)^2} \\ \hat b=\frac{\sum_{t=1}^n x_t y_t}{\sum_{t=1}^n x_t^2} \\ \hat c=\frac{n\sum_{t=1}^n x_t^2 y_t-\sum_{t=1}^n x_t^2 \sum_{t=1}^n y_t}{n\sum_{t=1}^n x_t^4-(\sum_{t=1}^n x_t^2)^2} \end{cases}$ (3.2.5)

　　2) 预测步骤

　　例3.4某公司1995～2003年的商品销售收入如表3.4所示，试预测该公司2004年的销售收入。

表3.4某公司1995～2003年商品销售收入数据表 (单位：万元)
年份	1995	1996	1997	1998	1999	2000	2001	2002	2003
销售收入	545	641	764	923	1107	1322	1568	1836	2140

　　解：

　　①绘制散点图如图3.3所示。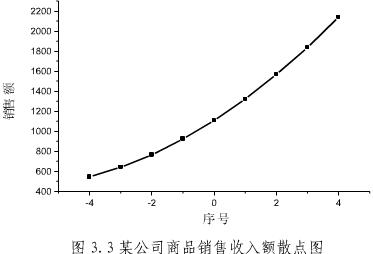

　　②根据观察值的散点图的变化趋势确定其属于二次曲线变化趋势后，列表计算二次曲线待定参数所需的数据。计算结果如表3.5所示。

　　③计算待定参数，建立预测模型，并计算预测值。

　　利用表3.5中的有关数据，代入式（3.2.5）中，计算得：

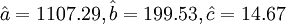
　　 $\hat a=1107.29,\hat b=199.53,\hat c=14.67$

　　该例的二次曲线的趋势外推预测模型为：

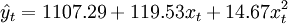　　 $\hat y_t=1107.29+119.53 x_t+14.67 x_t^2$ （3.2.6）

　　当x_t=5时，代入上式得

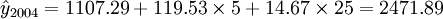　　 $\hat y_{2004}=1107.29+119.53\times 5+14.67\times 25=2471.89$ （万元）

表3.5某公司商品销售收入及有关数据计算表（单位：万元）
年份	$x t$	销售额 $y t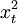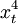$	$x_t^2$	$x_t^4$	$x t y t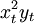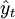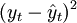$	$x_t^2 y_t$	$\hat y_t$	$(y_t-\hat y_t)^2$
1995	-4	545	16	256	2180	8720	543.89	1.23
1996	-3	641	9	81	-1923	5769	640.73	0.07
1997	-2	764	4	16	-1528	3056	766.91	8.47
1998	-1	923	1	1	-923	923	922.43	0.32
1999	0	1107	0	0	0	0	1107.29	0.08
2000	1	1322	1	1	1322	1322	1321.49	0.26
2001	2	1568	4	16	3136	6272	1565.03	8.82
2002	3	1836	9	81	5508	16524	1837.91	3.65
2003	4	2140	16	256	8560	34240	2140.13	0.02
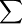$\sum$	0	10846	60	708	11972	76826		22.92