匈牙利解法

出自 MBA智库百科(https://wiki.mbalib.com/)

匈牙利解法（Hungarian method）

　　匈牙利解法是求解指派問題的一種新穎而又簡便的解法，它是美國數學家庫恩(Kuhn)於1955年提出的．庫恩引用了匈牙利數學家康尼格(Konig)一個關於矩陣中0元素的定理：繫數矩陣中獨立0元素的最多個數等於能覆蓋所有0元素的最小直線數，這種解法稱為匈牙利法．

　　指派問題的最優解有這樣一個性質，若從繫數矩陣的一行(列)各元素中分別減去該行(列)的最小元素，得到新矩陣，那麼以新矩陣為繫數矩陣求得的最優解和用原矩陣求得的最優解相同．利用這個性質，可使原繫數矩陣變換為含有很多0元素的新矩陣，而最優解保持不變．

　　具體操作為第一步：使指派問題的繫數矩陣經變換，在各行各列中都出現0元素．(1)從繫數矩陣的每行元素減去該行的最小元素；(2)再從所得繫數矩陣的每列元素中減去該列的最小元素．第二步：進行試指派．若此時得到的mPn，應回到第一步，重新對繫數矩陣進行變換。但要把第一步的過程改為(1)從繫數矩陣的每列元素減去該列的最小元素；(2)再從所得繫數矩陣的每行元素中減去該行的最小元素．這樣做就使得新矩陣的0元素比較多些．再進入第二步進行試指派就可以得到最優解．利用前面的性質可以證明這個最優解就是我們所要求的原問題的最優解，從而使得求解變得更為簡捷。

　　其基本原理是：為了實現目標極小，在繫數矩陣元素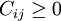的條件下，如果能使矩陣具有一組處於不同行又不同列的零元素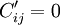（）打上括弧（），對應該元素的決策變數x_ij = 1，未打括弧元素對應的決策變數X_ij = 0，那麼目標函數值為最小，這樣的組合解就是最優解。

　　定理1：從(c_ij)矩陣的每行(或列)減去或加上一個常數u_i(或v_j)構成新矩陣(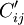)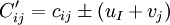，，則對應(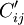)的(xij)最優解與原(c_ij)的最優解等價。

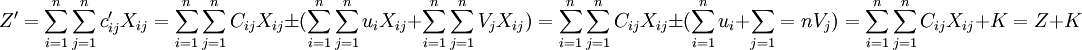
　　證明：如從新矩陣中得到最優解(x_ij)，則其目標函數值達到極值：其中：K為一常數，故當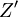達到極值時Z也達到極值。所以(x_ij）也為原矩陣(c_ij)的最優解。

　　利用這個定理，可以使原繫數矩陣(C_ij)變換成含有很多0元素的新繫數矩陣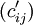，從而最優解保持不變。

　　獨立的0元素：在繫數矩陣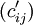中，位於不同行不同列的0元素。

　　若能在繫數矩陣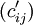中找出n個獨立的0元素,則令解矩陣(Xij)中對應這n個獨立0元素的取值為1，其他元素取值為0。將其代入目標函數中得到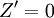,因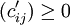,故它一定是最小值。這就是以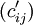為繫數矩陣的分派問題的最優解，也就是原問題的最優解。

　　匈牙利法只適用於符合以下三個條件的分派問題的求解：

　　① 目標函數為極小型；

　　② 繫數矩陣為方陣；

　　③ 繫數矩陣元素值非負。即：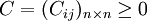

　　對於不滿足上述三個條件的分派問題應轉化為標準指派問題。

　　1）當分派問題目標要求極大時，即求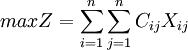,此時，可把求極大型轉變為求極小型，利用式：

　　max = Z = min( − Z)即：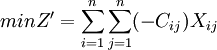

　　再由定理1，矩陣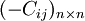每行均可加上一個常數M(或令C_ij中最大元素為M即可)，令：b_ij = M − C_ij，這時繫數矩陣可變換為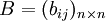：這時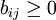，，B叫C的縮減矩陣。符合匈牙利法的條件。由定理1可知：所得的最小解就是原問題的最大解。

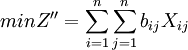
　　（2）繫數矩陣不是方陣，目標仍為Min型問題：繫數矩陣化為方陣。

　　其特點是：m個人分派做n項工作，繫數矩陣(C_ij)為m×n矩陣，m≠n。

　　①若 m < n ，則增添虛構的 s = n – m 行，補成方陣，但是對應的C_ij = 0。

　　②若 m > n ，則增添虛構的 s = m – n 列，補成方陣，但是對應的C_ij = 0。

　　步驟一：將這繫數矩陣進行變換，使各行各列都出現0元素．從繫數矩陣的每行元素減去該行的最小元素即得每行每列都有有0元素的繫數矩陣．

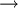
　　步驟二：進行試指派，找出獨立的0元素．獨立0元素用Θ表示，其它0用Φ表示得到

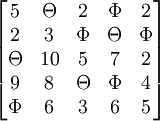　　……(1)

　　這裡Θ的個數m=4,而n=5；問題沒有得到求解，運用步驟三繼續求解．

　　步驟三：作最少的直線覆蓋所有的0元素，以確定該繫數矩陣中能找到最多的獨立元素數．為此按以下步驟進行．

　　(1)對沒有Θ的行打√號：；

　　(2)對已打√號的行中所含0元素的列打√號；

　　(3)再對所有打√號的列中的含有@元素的行打√號；

　　(4)重覆2、3直到得不出新的打√號的行列為止．

　　(5)對沒有打√號的行畫一橫線，有打√號的列畫一縱線，這就得到覆蓋所有0元素的最少直線數．

　　令直線數為l．若l < n，說明必須再變換當前的繫數矩陣，才能找到n個獨立的0元素，為此轉換步驟四；若l = n，而m < n，應回到步驟二，另行試探．

　　在此例中，對矩陣(1)按以下次序進行：

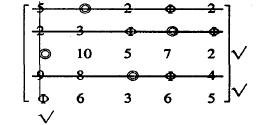
　　先在第五行旁打√，接著可判斷應在第一列下打√，接著在第3行旁打√，經檢查不能再打√了．對沒有打√行畫一直線以覆蓋0元素，對打√的列畫一直線以覆蓋0元素，得：

　　……(2)

　　由此可見l = 4 < n．所以應繼續對(2)矩陣進行變換轉步驟四．

　　步驟四：對(2)矩陣進行變換的目的是增加0元素．

　　為此在沒有被直線覆蓋的部分中找出最小元素．然後在打√行各元素中都減去這個最小元素，而在打√列的各元素上都加上這個最小元素，以保證原來0元素不變．這樣得到新繫數矩陣(它的最優解和原問題相同)．若得到n個獨立的0元素，則已得最優解，否則回到步驟三重覆進行．

　　在矩陣(2)中，在沒有被覆蓋部分(第3、5行)中找到最小元素為2，然後在第3、5行各元素分別減去2。給第l列各元素加2，得到新矩陣(3)

　　……(3)

　　按步驟二，找出所有的獨立0元素。得到矩陣(4)

　　……(4)

　　它具有n個獨立0元素．這就得到了最優解，相應解矩陣為

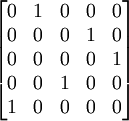
　　由解矩陣得最優指派方案：

　　甲——B，乙——D，丙——E，丁——C，戊——A

　　所需總時間為minz=32．