或然率
出自 MBA智库百科(https://wiki.mbalib.com/)
或然率（Probability）
目录 |
或然率即或然比，也叫概率和机会率：是对可能性在量上的一种科学说明和测定。它是要测定的偶然事件的数目与全部可能发生的偶然事件的总数之间的比率。如果n是可能发生的偶然事件的总数，而m是要测定的偶然事件的数目，那么，或然率就是m／n。m和n的比值在零和一之间，如果或然率等于零，就说明没有可能或不可能；如果或然率等于一，就说明有百分之百的可能，这时的可能就完全成了必然。测定或然率是人们实践的需要，目前在自然科学和社会科学中得到广泛的应用。
或然率有下列两种理论：
一、理论或然率（Theoretical Probability）：即根据事件本性推理而得的或然率，又称先天（Priori）或然率。例如：一枚硬币有正反两面，将其抛掷，其正面朝上之或然率，不待试验即可推知其为二分之一；又例如：若一摸彩箱中共有彩券三十张，其中有奖之彩券共十张，则可推知其中奖之或然率为三分之一。
二、经验或然率（Empirical Probability）：即根据实际现象归纳众多次数而得之或然率。例如：将一枚硬币抛掷一百次，若其出现正面朝上之次数为五十二次，即称抛掷该枚硬币出现正面朝上之或然率为52/100=0.52；又例如：若甲县某年内共出生婴儿四千八百六十五人，其中男婴为二千五百三十四人，则该县男婴出生之或然率即为2534/4865=0.52。此种或然率又称后天的（Posteriori）或然率。
或然率的公理[1]
或然率具有三个基本公理：
公理1：P{A}≥0 P{A}代表事件A发生的或然率，这个公理表示一个事件发生的或然率必须大于0或等于0。如果一个事件A可能发生，那么它的或然率P{A}必然大于0，假使事件A不可能出现，则它发生的或然率等干0。换句话说，任何一事件发生的或然率不可能是负值。
公理2：P{S}=1，S代表所有可能发生的全部事件，P{S}代表它们发生的或然率。这个公理表示在所有可能发生的各个事件中，必然有一个事件发生的或然率等于1。例如一个硬币只有正，反两面，投掷的结果不是正面就是反面，所有可能发生的事件共有二个，一个是出现正面，一个是出现反面。用S代表所有可能发生的事件的全体，那么用A表示正面，用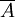
表示反面，这样S与A、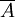三者的关系可以表示为
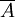(U这个符号读作“并”，意思指“或者”即A或至少有一个发生。在这里的作用与加法符号相同)。这样投掷一枚硬币出现正面与反面的或然率就可以写作
假设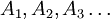
这样一些事件不能并存，互相排斥，就可以用
表示事件同时发生不存在，也就是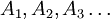等事件同时出现是不可能的。(
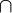这个符号读作“交”表示“乘积”指A1和A2和A3等事件同时发生)。由此可得：
公理3: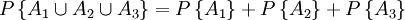
公理3表示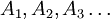这些事件中任一事件都不能与其它事件同时并存，则A1、A2、A3事件发生的或然率等于各个事件发生或然率之和。
或者若事件A两两互不相容，若事件1,A2,…两两互不相容，则有P(A+A+L=P(A)+P(A)+L)。
例如；在一个袋中有各色的小球10个，仅知道其中有红球A1一个，白球A2二个，兰球A3三个，这三个事件是互相排斥，也就是说是白球就不可能是红球，是红球就不可能是兰球。如果从袋中抽取一个球，问这个球是红、白、兰三色中任何一色时的或然率为多少?根据公理3得
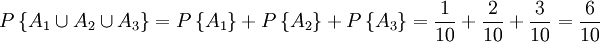
- ↑ 曹毓侯.《统计学》辅导 第一册[M].中国展望出版社,1983年08月第1版.
评论(共12条)
因为PA包含PA1-PA3.PA系整体
因为PA包含PA1-PA3.PA系整体
PA1∩A2∩A3.∩系指相同的部分。
应该是表述让人有些误解，就是说公理三是有前提的，就是事件A1，A2，A3……不能同时发生，即互斥，然后才有公理三的公式成立。这个是概率论互斥事件的性质。不应该说成公理吧。求贡献者答疑。
应该是表述让人有些误解，就是说公理三是有前提的，就是事件A1，A2，A3……不能同时发生，即互斥，然后才有公理三的公式成立。这个是概率论互斥事件的性质。不应该说成公理吧。求贡献者答疑。
我增加了一些内容，看是否符合。而且这个算是概率的公理化定义或者说是用性质来定义的。MBA智库百科是人人都可以参与的编辑，欢迎您的加入。
恩，是公理化定义，今天我刚好听说是俄国/俄罗斯的统计学家对统计学进行公理化定义，归纳了三条定理。多谢。
是的。如果你有什么资料也可以自己参与编辑修改的，谢谢您的关注。
公理3那裡不是很明白 為何PA1∪A2∪A3代表不能與其他共存 不是應該 PA1∩A2∩A3 嗎?