狀態空間模型

出自 MBA智库百科(https://wiki.mbalib.com/)

狀態空間模型(state space model)

　　狀態空間模型是動態時域模型，以隱含著的時間為自變數。狀態空間模型在經濟時間序列分析中的應用正在迅速增加。其中應用較為普遍的狀態空間模型是由Akaike提出並由Mehra進一步發展而成的典型相關(canonical correlation)方法。由Aoki等人提出的估計向量值狀態空間模型的新方法能得到所謂內部平衡的狀態空間模型，只要去掉系統矩陣中的相應元素就可以得到任何低階近似模型而不必重新估計，而且只要原來的模型是穩定的，則得到的低階近似模型也是穩定的。

　　狀態空間模型起源於平穩時間序列分析。當用於非平穩時間序列分析時需要將非平穩時間序列分解為隨機游走成分(趨勢)和弱平穩成分兩個部分分別建模。 含有隨機游走成分的時間序列又稱積分時間序列，因為隨機游走成分是弱平穩成分的和或積分。當一個向量值積分序列中的某些序列的線性組合變成弱平穩時就稱這些序列構成了協調積分(cointegrated)過程。 非平穩時間序列的線性組合可能產生平穩時間序列這一思想可以追溯到回歸分析，Granger提出的協調積分概念使這一思想得到了科學的論證。 Aoki和Cochrane等人的研究表明：很多非平穩多變數時間序列中的隨機游走成分比以前人們認為的要小得多，有時甚至完全消失。

　　協調積分概念的提出具有兩方面的意義：

　　① 如果一組非平穩時間序列是協調積分過程，就有可能同時考察他們之間的長期穩定關係和短期關係的變化；

　　② 如果一組非平穩時間序列是協調積分過程，則只要將協調回歸誤差代入系統狀態方程即可糾正系統下一時刻狀態的估計值，形成所謂誤差糾正模型。

　　Aoki的向量值狀態空間模型在處理積分時間序列時，引入了協調積分概念和與之相關的誤差糾正方法，因此向量值狀態空間模型也是誤差糾正模型。 一個向量值時間序列是否為積分序列需判斷其是否含有單位根，即狀態空間模型的動態矩陣是否含有量值為1的特征值。 根據動態矩陣的特征值即可將時間序列分解成兩個部分，其中特征值為1的部分(包括接近1的“近積分”部分)表示隨機游走趨勢，其餘為弱平穩部分，兩部分分別建模就得到了兩步建模法中的趨勢模型和周期模型。

　　狀態空間模型的假設條件是動態系統符號馬爾科夫特性，即給定系統的現在狀態，則系統的將來與其過去獨立。

　　狀態空間模型包括兩個模型：一是狀態方程模型，反映動態系統在輸入變數作用下在某時刻所轉移到的狀態；二是輸出或量測方程模型，它將系統在某時刻的輸出和系統的狀態及輸入變數聯繫起來。

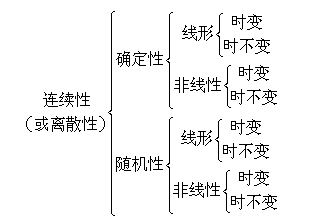
　　狀態空間模型按所受影響因素的不同分為：（1）確定性狀態空間模型；（2）隨機性狀態空間模型

　　狀態空間模型按數值形式分為：（1）離散空間模型；（2）連續空間模型

　　狀態空間模型按所描述的動態系統可以分為（1）線性的與非線性的；（2）時變的與時不變的。

　　狀態空間模型具有如下特點：

　　1、狀態空間模型不僅能反映系統內部狀態，而且能揭示系統內部狀態與外部的輸入和輸出變數的聯繫。

　　2、狀態空間模型將多個變數時間序列處理為向量時間序列，這種從變數到向量的轉變更適合解決多輸入輸出變數情況下的建模問題。

　　3、狀態空間模型能夠用現在和過去的最小心信息形式描述系統的狀態，因此，它不需要大量的歷史數據資料，既省時又省力。

　　1）狀態空間模型不僅能反映系統內部狀態，而且能揭示系統內部狀態與外部的輸入和輸出變數的聯繫。

　　2）狀態空間模型將多個變數時間序列處理為向量時間序列，這種從變數到向量的轉變更適合解決多輸入輸出變數情況下的建模問題。

　　3）狀態空間模型能夠用現在和過去的最小信息形式描述系統的狀態，因此，它不需要大量的歷史數據資料，既省時又省力。