HSD檢驗法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是HSD檢驗法[1]
J·W·圖凱(Tukey)於1953年提出一種能將所有各對平均值同時比較的方法,這種方法現在已被廣泛採用,一般稱之為“HSD檢驗法”,或稱“W法”。
採用圖凱檢驗法時,只要計算一個數值,就能藉以完成所有各對平均值之差的比較。這個數值稱為HSD,由以下公式給出:
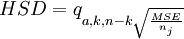
其中的q值與顯著性水平α,實驗中平均值的個數k以及誤差自由度n-k有關,可由附表E查出。任何一對平均值之差只要超過HSD值,就表明這一對平均值之間的差別是顯著的。
註意,統計量HSD要求所有樣本的容量都相等,即要求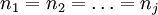 。
。
案例一:[1]
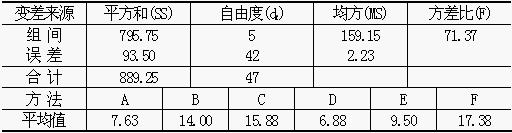
為了對生產某種化合物的6種方法作比較,進行了一項實驗,得到的數據列於下表。感興趣的變數是這種化合物中固體物質的含量百分比。每種方法都有8個觀察值。假定在顯著性水平α=0.05之下,通過方差分析所算出的F是顯著的。現在,產生的合乎邏輯的問題恰好就是什麼地方出現了顯著差別的問題。
方差分析表
解:圖凱檢驗法能為這個問題提供答案。
在把圖凱的HSD方法應用於上表中的數據之前,我們先把各對平均值之差的絕對值列成下表。下表中行和列中的樣本處理平均值均按由大到小的數值順序排列,下表中給出相應的差值。
諸平均值之差的絕對值
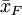 | 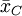 | 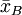 | 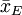 | 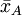 | 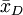
| |
|---|---|---|---|---|---|---|
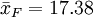 | - | 1.50 | 3.38 | 7.88 | 9.75 | 10.50 |
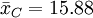 | - | 1.88 | 6.38 | 8.25 | 9.00 | |
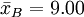 | - | 4.50 | 6.37 | 7.12 | ||
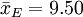 | - | 1.87 | 2.62 | |||
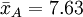 | - | 0.75 | ||||
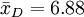 | - |
如果選擇顯著性水平α=0.05,便可從附表E查出q0.05,6,42 = 4.22(自由度可在40與60之間作內插)。從上表可找到MSE=2.23,於是,算出:
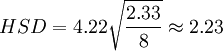
當我們將上表中各種平均值之差同2.23比較時,發現只有以下幾對平均值之差不顯著:
其餘差值都是顯著的。
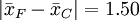
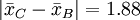
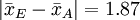
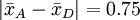






附表H是什麼表?