田口方法
出自 MBA智库百科(https://wiki.mbalib.com/)
田口方法（Taguchi Methods）
目錄 |
田口方法是一種低成本、高效益的質量工程方法，它強調產品質量的提高不是通過檢驗，而是通過設計。田口方法是日本田口玄一博士創立的，其核心內容被日本視為“國寶”。日本和歐美等發達國家和地區，儘管擁有先進的設備和優質原材料，仍然嚴把質量關，應用田口方法創造出了許多世界知名品牌。
隨著市場競爭的日趨激烈，企業只有牢牢把握市場需求，用較短的時間開發出低成本、高質量的產品，才能在競爭中立於不敗之地。在眾多的產品開發方法中，田口方法不失為提高產品質量，促進技術創新，增強企業競爭力的理想方法。
田口方法的目的在於，使所設計的產品質量穩定、波動性小，使生產過程對各種雜訊不敏感。在產品設計過程中，利用質量、成本、效益的函數關係，在低成本的條件下開發出高質量的產品。田口方法認為，產品開發的效益可用企業內部效益和社會損失來衡量．企業內部效益體現在功能相同條件下的低成本，社會效益則以產品進人消費領域後給人們帶來的影響作為衡量指標。假如，由於一個產品功能波動偏離了理想目標，給社會帶來了損失，我們就認為它的穩健性設計不好，而田口式的穩健性設計恰能在降低成本、減少產品波動上發揮作用。
田口方法的基本思想是把產品的穩健性設計到產品和製造過程中，通過控制源頭質量來抵禦大量的下游生產或顧客使用中的雜訊或不可控因素的干擾，這些因素包括環境濕度、材料老化、製造誤差、零件間的波動等等。田口方法不僅提倡充分利用廉價的元件來設計和製造出高品質的產品，而且使用先進的試驗技術來降低設計試驗費用，這也正是田口方法對傳統思想的革命性改變．為企業增加效益指出了一個新方向。
與傳統的質量定義不同，田口玄一博士將產品的質量定義為：產品出廠後避免對社會造成損失的特性，可用“質量損失”來對產品質量進行定量描述。質量損失是指產品出廠後“給社會帶來的損失”，包括直接損失（如空氣污染、雜訊污染等）和間接損失（如顧客對產品的不滿意以及由此導致的市場損失、銷售損失等）。質量特性值偏離目標值越大，損失越大，即質量越差，反之，質量就越好。對待偏差問題，傳統的方法是通過產品檢測剔除超差部分或嚴格控制材料、工藝以縮小偏差。這些方法一方面很不經濟，另一方面在技術上也難以實現。田口方法通過調整設計參數，使產品的功能、性能對偏差的起因不敏感，以提高產品自身的抗干擾能力。為了定量描述產品質量損失，田口提出了“質量損失函數”的概念，並以信噪比來衡量設計參數的穩健程度。
由此可見，田口方法是一種聚焦於最小化過程變異或使產品、過程對環境變異最不敏感的實驗設計方法，是一種能設計出環境多變條件下能夠穩健和優化操作的高效方法。
田口方法的特色主要體現在以下幾個方面：
(1)“源流”管理理論。田口方法認為，開發設計階段是保證產品質量的源流，是上游，製造和檢驗階段是下游。在質量管理中，“抓好上游管理，下游管理就很容易”，若設計質量水平上不去，生產製造中就很難造出高質量的產品。
(2)產品開發的三次設計法。產品開發設計(包括生產工藝設計)可以分為三個階段進行，即系統設計、參數設計、容差設計。參數設計是核心，傳統的多數設計是先追求目標值，通過篩選元器件來減少波動，這樣做的結果是，儘管都是一級品的器件，但整機由於參數搭配不佳而性能不穩定。田口方法則先追求產品的穩定性，強調為了使產品對各種非控制因素不敏感可以使用低級品元件．通過分析質量特性與元部件之間的非線性關係(交互作用)．找出使穩定性達到最佳水平的組合。產品的三次設計方法能從根本上解決內外干擾引起的質量波動問題，利用三次設計這一有效工具，設計出的產品質量好、價格便宜、性能穩定。
(3)質量與成本的平衡性。引入質量損失函數這個工具使工程技術人員可以從技術和經濟兩個方面分析產品的設計、製造、使用、報廢等過程，使產品在整個壽命周期內社會總損失最小。在產品設計中，採用容差設計技術，使得質量和成本達到平衡，設計和生產出價廉物美的產品，提高產品的競爭力。
(4)新穎、實用的正交試驗設計技術。使用綜合誤差因素法、動態特性設計等先進技術，用誤差因素模擬各種干擾(如雜訊)，使得試驗設計更具有工程特色，大大提高試驗效率，增加試驗設計的科學性，其試驗設計出的最優結果在加工過程和顧客環境下都達到最優。採用這種技術可大大節約試驗費用。
田口方法是一門實用性很強的技術，在生產實踐中特別是產品開發設計中顯示出強大的生命力,其魅力主要表現為：
(1)提高產品科技含量，促進技術創新。通過採用田口方法可改變企業一味引進先進設備的狀況，增強二次創新能力，進而提高產品開發能力。
(2)可縮短產品開發周期，加速產品更新換代。應用田口方法可在質量管理中提高生產率，收到事半功倍的效果。
(3)應用田口方法創名牌。使用田口方法的三次設計技術設計出來的產品穩健性好，抵禦外界干擾的能力強，波動小，質量可靠，易於創出知名產品，占領市場，打出自己的品牌。
(4)應用田口方法創效益。田口方法用廉價的三等品零件組裝一等品整機，真正做到了價廉物美，使企業的經濟效益更上一個臺階。
現今在發達國家田口方法已運用得相當廣泛，並且為它們創造了不斐的收益。中國的一些企業也引進了這種先進方法並取得了良好的收效。深圳建裕電子公司就是應用田口方法走產品開發和技術創新之路的成功範例。建裕從日本、臺灣等比較先進、發達的地區引進國內外先進的電路，進行吸收、提高和創新，在市場調查的基礎上開發出性能更可靠、功能更齊全、價格更合理的電話機。使用田口方法後，他們每兩個月就推出一部新款的電話機，產品物美價廉，很受用戶的青睞，市場份額不斷擴大，知名度不斷提高，多次被用戶評為“消整者信得過產品”，在激烈競爭的電話市場中牢牢地站穩腳跟。
- 田口方法的實施步驟可分為下列十項：
1.選定品質特性
2.判定品質特性之理想機能
3.列出所有影響此品質特性的因數
4.定出信號因數的水準
5.定出控制因們的水準
6.定出干擾因數的水準，必要的話，進行干擾實驗
7.選定適當的直交表，並安排完整的實驗計劃
8.執行實驗，記錄實驗數據
9.資料分析
10.確認實驗
SPC與田口方法[1]
SPC與田口方法同屬質量控制領域改進質量的方法，田口方法屬於產品設計階段的設計質量方法，而SPC 是在產品製造階段的監控質量方法。 產品質量首先是設計出來的，其次才是製造出來的，田口方法保證了設計產品質量的穩健性，在製造過程中SPC使產品保持在設計水平上，同時，通過控製圖監測波動的大小，提供進一步改進設計質量的信息。 因此，二者配合在產品的不同階段改進質量，以增強企業的質量競爭力。
田口方法與EPC[1]
田口方法和EPC 同屬於質量優化方法，EPC 通過反饋補償原理最小化過程的波動，而田口方法通過利用正交實驗進行穩健的參數設計， 以最小化產品設計參數的波動。
傳統上， 田口方法大多應用在產品設計階段，但在現代複雜&動態的過程狀態下，如果要用EPC 對過程進行調整，就要在眾多的變數中選擇關鍵變數作為控制變數來設計調整控制器，而田口方法可以作為選擇關鍵變數的有效工具應用於製造階段，因此，為了有效地調整過程，可以首先應用田口方法選擇影響輸出的關鍵過程變數，然後，基於所選擇的關鍵變數設計調整控制器，二者整合同樣具有互補的作用。
案例一:基於田口方法的小批量生產過程式控制制[2]
一、引言
將田口方法引入軍工生產小批量生產過程式控制制與過程能力分析中,探討其可行性、優越性,以期提高兵器工業軍工生產的質量穩定性,過程式控制制方法的經濟性和有效性,為國防科技工業武器裝備的研製生產提供一種行之有效的過程式控制制方法。
二、田口式過程輸出的反饋控制理論
1.田口質量損失函數——經濟性評價基礎
田口式過程輸出的反饋控制是田口式線內質量工程技術中針對計量型過程輸出特性的一個分支,對應於休哈特計量值控製圖。它基於田口的波動質量觀和質量損失函數,是一種從經濟性角度考察質量水平的方法。在這裡,質量特性本身的波動損失和與其有關的質量管理、調整、檢測費用等被統一納入質量損失函數進行量化計算,使得質量水平及質量控制經濟性的改進效果一目瞭然(見式1)。
![L=\frac{B}{n}+\frac{C}{u}+\frac{A}{\Delta^2}[\frac{D^2}{3}+(\frac{n+1}{2}+l)\frac{D^2}{u}]](/w/images/math/1/a/0/1a0026f96b44b9ae3bffc4e7992dc655.png)
(1)
田口損失函數中各參數意義如下:產品的規格限m±Δ,單位產品不合格的損失A,對產品質量特性每次測量的費用B,測量間隔n,時滯(從取樣到完成檢測時間間隔內生產產品的個數)l,管理界限D,過程調整費用C,平均調整間隔u(註:各參數加下標0時表示現行水平)。
這樣,損失函數四部分的含義為:L=檢測費用+調整費用+規格限內波動損失+規格限外波動損失。前兩部分之和是管理成本,後兩部分之和為質量損失。這裡為了工程應用方便,認為控制限內的質量特性值大致為均勻分佈。
以損失函數為工具,謀求管理成本和產品質量損失的最佳平衡,從而使總損失(管理成本+質量損失)為最小,進行過程的反饋控制。這裡用簡單的微分求偏導即得到針對該過程的最佳控制方案(n,D),見式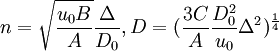(2)。
(2)
平均調整間隔的預測值為。
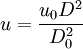(3)
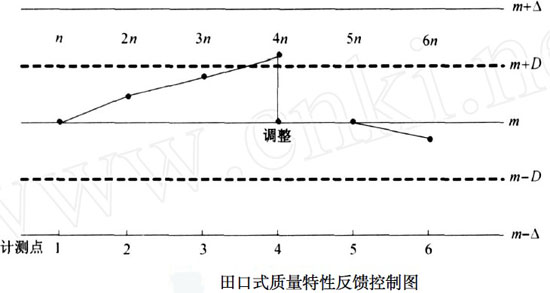
管理界限D即用於繪製田口式反饋控製圖(見下圖)
最後可以分別計算出當前及改進控制方案後的損失函數值,即可直觀地看到質量控制的改進收益。
2.相關假設
田口式過程輸出反饋控制主要有以下一些假設。
假設1 質量特性值為隨機變數,呈隨機徘徊或布朗分子運動的情形,由此可以推出平均調整間隔的預測值；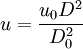
假設2 工序進程有一定的前因後果的隨機步游關係,質量特性值將隨時間而飄移(見上圖),由此當以測量間隔n檢查時發現前面的點在管理界限內,而這次的點在限外,認為其間的點是逐步偏出界限,且為均勻分佈,因而平均超出個數為(n+1)/2個；
假設3 從過程出現異常到被調整前持續生產不合格品,這一假設的直接體現是認為時滯1在調整界限外生產；
假設4 特性值在管理界限內大致呈均勻分佈,因而得到損失函數L中這部分的波動為D2 / 3。
3.田口式過程能力指數———有效性評價指標。
田口方法有其專門的過程能力指數,其理論形式如下。
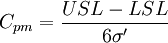(4)
其中，![\sigma^{\prime2}=E[(X-T)^2]=\sigma^2+(\mu-T)^2](/w/images/math/3/d/8/3d83af13a1c59c7fd46c3f41dd391d1b.png)
,T為質量特性的目標值。
機械加工中,為了便於上下工序銜接或裝配關係的要求,經常出現目標值不在規格中心的情況,而傳統的過程能力指數Cpk只考慮工序平均對規格中心的偏移,沒有考慮工序平均與目標值的偏移。田口式過程能力指數Cpm恰好彌補了這一點。實地調研中發現大多數工序的目標值都是有偏的,因此採用Cpm更符合實際。它完整地解釋了質量特性偏離目標值的原因:一是質量特性的波動σ,二是工序平均的偏移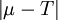
。
在實際應用中,Cpm的估計式為。
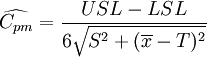(5)
式(5)為通用式,可以獨立於田口式過程式控制制使用。
三、小批量生產過程式控制制實證
1.現狀分析及優化效果預測
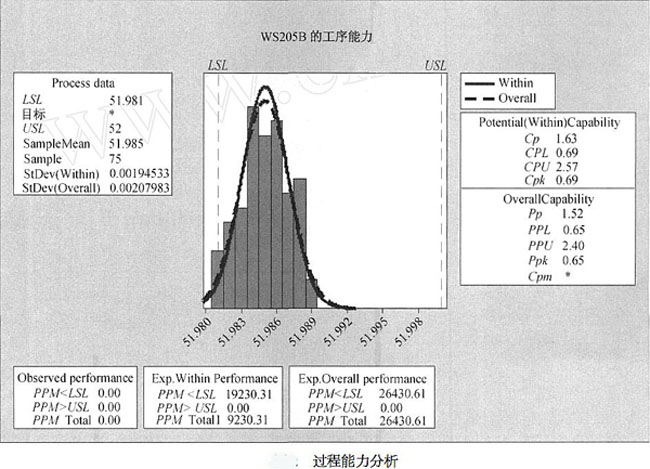
赴軍工企業實地調研時,選擇了某關鍵件06212/WS205B的生產工序作為試點工序收集數據,進行過程式控制制實驗。該產品該月共加工126件(質量特性的原始數據略),規格為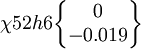
。該工序的過程式控制制目前使用休哈特控製圖。
從minitab軟體輸出的休哈特控製圖(略)上看,過程處於穩定受控狀態,無需進行調整。過程能力分析結果(下圖)顯示理論正態曲線基本覆蓋了直方圖,數據基本服從正態分佈。Cpk = 0.69,過程能力很低。因該工序質量特性為加工孔徑,故出現很明顯的下偏現象。
於該工序試點採用田口式反饋控制技術,在生產現場收集到以下數據資料。不合格品損失A為31.38元;單位產品測量費用B為1元;時滯l為1件;過程調整費用C為100元;現行測量間隔n0為1件;現行管理界限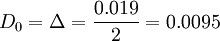
。
由於實驗工序批量小,生產周期較長,無法取得現行平均調整間隔統計值u0的準確數值。故採用平均不合格品率的倒數1/p0來估計,p0由不合格品率與過程能力指數的關係求得。
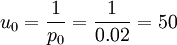件。
將以上參數代入式(2),得最佳反饋控制方案(n,D)為。
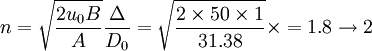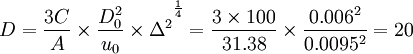件。
件。
過程增益為
優化後預計的損失函數值為
![L=\frac{B}{n}+\frac{C}{u}+\frac{A}{\Delta^2}[\frac{D^2}{3}+{\frac{n+1}{2}+l}\frac{D^2}{u}]=\frac{1}{2}+\frac{100}{20}+\frac{31.38}{0.0095^2}\cdot[\frac{0.006^2}{3}+{\frac{2+1}{2}+1}\frac{0.006^2}{20}]=0.5+5+4.1724+1.5647=11.2371](/w/images/math/f/a/5/fa5b2149a709b197fce2d3447898b1af.png)
(元)
損失函數值的現行水平為
![L_0=\frac{B}{n_0}+\frac{C}{u_0}+\frac{A}{\Delta^2}[\frac{D_0^2}{3}+{\frac{n_0+1}{2}+l}\frac{D_0^2}{u_0}]=\frac{1}{1}+\frac{100}{50}+\frac{31.38}{0.0095^2}[\frac{0.0095^2}{3}+{\frac{1+1}{2}+1}\frac{0.0095^2}{50}]=1+2+10.46+1.2552=14.7152](/w/images/math/3/9/a/39a5c77269d3e7324a89977c9b0f9479.png)
(元)
增益ΔL = L0 − L = 14.7152 − 11.2371 = 3.48(元)，若每月加工量與本月大致相當,均為120件左右,則全年該工序增益總額為3.48×120×12=5011.2元。
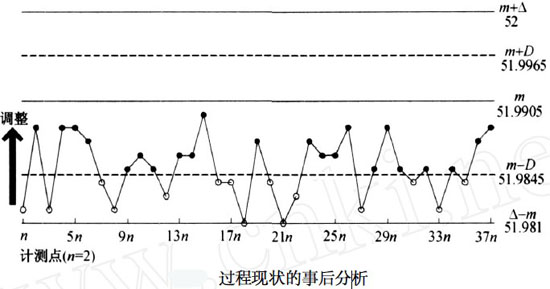
由於田口式反饋控制要求邊調整工序狀態邊畫圖,因此對成批收集到的以往數據只能作事後分析(見下圖)。
上圖可以稱作田口式的分析用控製圖,顯示了較多的需調整次數,與預測的平均調整間隔20差距很大。這主要是因為該圖為事後畫出,並未按照田口式控製圖的操作要求繪製。
2.後續實驗
在後續實驗中,邊調整工序邊畫田口式反饋控製圖,出現越界則暫停生產調整工序,使之由異常回覆到初始狀態。同時,要求生產線忽略加工習慣,完全按規格要求加工,並提高了測量精度。收集到的數據大致服從N:(51.9905,0.00412),獲得40個左右計量點。
由於其它過程參數不變,根據田口式反饋控制計算的最佳測量間隔為n=2,上下管理界限為(51.9845,51.9965)。
第一批數據從第1個數據51.9922開始計量描點,在第11個描點處出現越界值51.9817,停止生產調整工序到初始狀態,然後重新收集數據。
第二批數據從第1個數據51.9867開始計量描點,到第8個描點處出現越界值51.9770,停止生產調整工序到初始狀態,然後重新收集數據。
第三批數據從第1個數據51.9864開始計量描點,到第3個描點處出現越界值51.9825,停止生產調整工序到初始狀態,然後重新收集數據。
……(依次類推,下略)
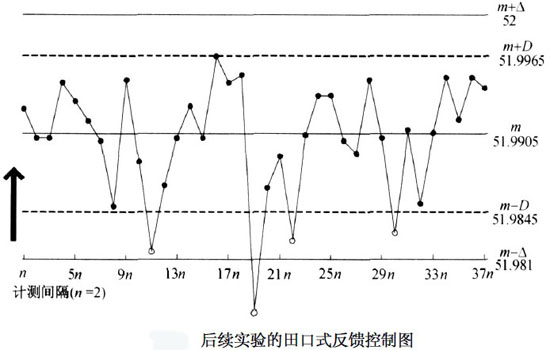
最後畫出的田口式反饋控製圖如下圖。該圖為邊調整邊繪製,故可稱為控制用反饋控製圖。
後續實驗分批數據
| 第一批 | 第二批 | 第三批 | 第四批 | 第五批 |
| 51.9922 | 51.9867 | 51.9864 | 51.9904 | 51.9908 |
| 51.9903 | 51.9903 | 51.9888 | 51.9932 | 51.9851 |
| 51.9902 | 51.9926 | 51.9825 | 51.9933 | 51.9906 |
| 51.9944 | 51.9903 | 51.9900 | 51.9948 | |
| 51.9930 | 51.9965 | 51.9890 | 51.9916 | |
| 51.9914 | 51.9943 | 51.9946 | 51.9949 | |
| 51.9899 | 51.9950 | 51.9903 | 51.9941 | |
| 51.9850 | 51.9770 | 51.9830 | ||
| 51.9946 | ||||
| 51.9884 | ||||
| 51.9817 |
前面計算出的最佳調整間隔預測值u=20件,即在75件產品中大約會出現4次調整,圖4顯示的情況與理論計算基本吻合。Cpm=1.67,單件產品質量損失=11.24元,過程式控制制的有效性和經濟性都得到了明顯改善。
應用田口方法對軍工生產中小批量生產過程進行了試點實驗數據收集、處理,通過改換過程式控制制方式,提高了小批量生產過程式控制制方法的經濟性和有效性,並制訂了田口式反饋控製圖的標準作業指導書(限於篇幅未附)。其操作方法簡單,評價結果直觀,更易為現代企業所接受。
能否搞個案例啊