线性回归预测法

出自 MBA智库百科(https://wiki.mbalib.com/)

线性回归(linear regression)

　　所谓线性回归模型就是指因变量和自变量之间的关系是直线型的。 回归分析预测法中最简单和最常用的是线性回归预测法。

　　回归分析是对客观事物数量依存关系的分析是数理统计中的一个常用的方法． 是处理多个变量之间相互关系的一种数学方法。

　　在现实世界中，我们常与各种变量打交道，在解决实际问题过程中，我们常常会遇到多 个变量同处于一个过程之中，它们之间互相联系、互相制约。常见的关系有两种：一类为 “确定的关系”即变量间有确定性关系，其关系可用函数表达式表示．例如：路程s,时间t, 与速度v之间有关系式：s=vt 在圆体给与半径r之间有关系式v= 另外还有一些变量．他们之 间也有一定的关系，然而这种关系并不完全确定，不能用函数的形式来表达，在这种关系中 至少有一个变量是随机的．例如：人的身高与体重有一定的关系，一般来讲身高高的人体重 相对大一些．但是它们之间不能用一个确定的表达式表示出来．这次变量（或至少其中有一 个是随机变量）之间的关系．我们称之为相关关系．又如环境因素与农作物的产量也有 相关关系，因为在相同环境条件下 农作物的产量也有区别，这也就是说农作物的产量是一个 随机变量．回归分析就是研究相关关系的一种数学方法，是寻找不完全确定的变量间的数学 关系式并进行统计推断的一种方法．它能帮助我们从一个变量取得的值去估计另一个变量的 值．在这种关系中最简单的是线性回归。

　　线性回归分析是对客观事物数量关系的分析，是一种重要的统计分析方法，被广泛的应 用于社会经济现象变量之间的影响因素和关联的研究．由于客观事物的联系错综复杂经济现 象的变化往往用一个变量无法描述， 故本篇论文在深入分析一元线性回归及数学模型的情况 下，又详细地介绍了多元线性回归方程的参数估计和其显著性检验等．全面揭示了 这种复杂的依存关系，准确测定现象之间的数量变动．以提高预测和控制的准确度．

　　一元线性回归分析预测法，是根据自变量x和因变量Y的相关关系，建立x与Y的线性回归方程进行预测的方法。由于市场现象一般是受多种因素的影响，而并不是仅仅受一个因素的影响。所以应用一元线性回归分析预测法，必须对影响市场现象的多种因素做全面分析。只有当诸多的影响因素中，确实存在一个对因变量影响作用明显高于其他因素的变量，才能将它作为自变量，应用一元相关回归分析市场预测法进行预测。

　　一元线性回归分析法的预测模型为：

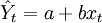　　　　　　（1）

　　式中，x_t代表t期自变量的值；

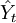　　代表t期因变量的值；

　　a、b代表一元线性回归方程的参数。

　　a、b参数由下列公式求得（用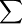代表）：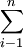

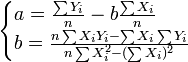
　　为简便计算，我们作以下定义：

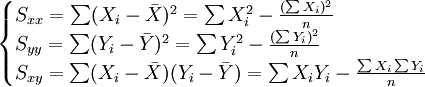　　　　　　(2)

　　式中：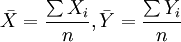

　　这样定义a、b后，参数由下列公式求得：

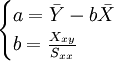　　　　　　(3)

　　将a、b代入一元线性回归方程Y_t = a + bx_t，就可以建立预测模型，那么，只要给定x_t值，即可求出预测值。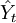

　　在回归分析预测法中，需要对Ｘ、Ｙ之间相关程度作出判断，这就要计算相关系数r，其公式如下：

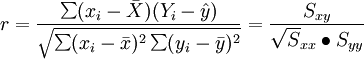
　　相关系数r的特征有：

　　①相关系数取值范围为：-1≤r≤1 。

　　②r与b符合相同。当r>0，称正线性相关，X_i上升，Y_i呈线性增加。当r<0，称负线性相关，X_i上升，Y_i呈线性减少。

　　③|r|=0，X与Y无线性相关关系；|r|=1，完全确定的线性相关关系；0<|r|<1，X与Y存在一定的线性相关关系；|r|>0.7，为高度线性相关；0.3<|r|≤0.7，为中度线性相关；|r|≤0.3，为低度线性相关。

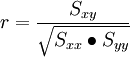　　　　　　(4)

　　多元线性回归预测模型一般公式为：

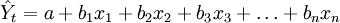
　　多元线性回归模型中最简单的是只有两个自变量（n=2）的二元线性回归模型，其一般形式为：

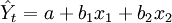
　　下面以二元线性回归分析预测法为例，说明多元线性回归分析预测法的应用。

　　二元线性回归分析预测法，是根据两上自变量与一个因变量相关关系进行预测的方法。二元线性回归方程的公式为：

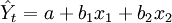　　 　　　　　　　　(1)

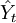　　式中：：因变量；

　　x₁,x₂：两个不同自变量，即与因变量有紧密联系的影响因素。

　　a,b₁,b₂：是线性回归方程的参数。

　　a,b₁,b₂是通过解下列的方程组来得到。

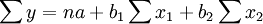
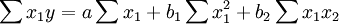　　　　　　　　　　(2)

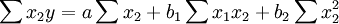
　　二元线性回归预测法基本原理和步骤同一元线性回归预测法没有原则的区别，大体相同。

• 非线性回归预测法
• 一元线性回归预测法
• 多元线性回归预测法