算术平均数
出自 MBA智库百科(https://wiki.mbalib.com/)
算术平均数(Arithmetic Average)
目录 |
算术平均数(算术平均法)是总体各单位某一数量标志的平均数。通过算术平均数,可以用来求出一定观察期内预测目标的时间数列的算术平均数作为下期预测值的一种最简单的时序预测法。
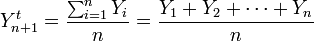
式中,
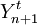 =第n+1期销售量的预测值
=第n+1期销售量的预测值
Yi=第i期的实际销售量
n=所选期数
基本计算公式为:
1、简单算术平均法
2、加权算术平均法
该方法的优点是计算简单,而缺点是计算平均数时没有考虑到近期的变动趋势,因而预测值与实际值往往会发生较大的误差。
通常适用于预测销售比较稳定的产品。如没有季节性变化的粮油食品和日常用品等。
算术平均法根据企业过去按时间顺序排列的销售量(或销售额)的历史数据,计算其平均数,并将该平均数作为计划期的销售预测数。
其计算公式为:
计划期销售量(额)预测数=各期销售量(额)之和÷期数。
算术平均数与强度相对数的比较
1、概念不同。强度相对数是两个有联系而性质不同的总体指标值对比而形成相对数指标。算术平均数是反映同质总体各单位某一数量标志值一般水平的指标。
2、主要作用不同。强度相对数反映现象的密度、强度和普遍程度。算术平均数反映同一现象总体的一般水平。
3、分子分母的依存关系不同。算术平均数的分子与分母间存在直接的依存关系。强度相对指标的分子、分母之间无依存关系。
1、简单算术平均法
计算公式:
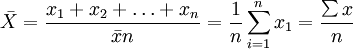
其中:---  算术平均数,X---各单位标志值(变量值),n---总体单位数(项数)。
算术平均数,X---各单位标志值(变量值),n---总体单位数(项数)。
运用条件:统计资料未分组时
例:某公司下属各店职工按工龄分组情况
工龄 组中值
x人 数 f 一店 二店 三店 四店 五店 0~2年
2 ~5年
5 ~10年
10 ~20年1.0
3.5
7.5
15.01
1
1
17
7
7
725
25
25
251
3
6
1010
6
3
1合计 — 4 28 100 20 20 平均工龄 — 6.75 6.75 6.75 10.325 3.425
2、加权算术平均法
计算公式:
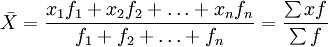
其中: ----代表算术平均数,x 代表各单位标志值(变量值),f 代表各组单位数(项数)。
----代表算术平均数,x 代表各单位标志值(变量值),f 代表各组单位数(项数)。
运用条件:统计资料分组时从前面的表中资料可以看出一、二、三店人数相差很远,但平均工龄相等。四、五店人数相等,但平均工龄相差很大。由此我们不难得出如下结论:平均数水平高低受两个因素的影响:
(1)受各组变量值( x )大小的影响
(2)受各组权数(f)大小的影响。(绝对权数表现为次数、频数,相对权数表现为频率)。
1、平均数与总体单位数的积等于总体标志总量
2、若每个变量值 (X ) 加减一任意常数α,则平均数也加减这个任意值α。
3、若每个变量值 (X)乘以一任意常数α,则平均数也乘以这个任意值α。
4、若每个变量值( X)除以一任意常数α,则平均数也除以这个任意值α。
5、各个变量值(X)与算术平均数 的离差和为零。
的离差和为零。
6、各个变量值(X)与算术平均数 的离差平方和为最小值。
的离差平方和为最小值。





