凸性
出自 MBA智库百科(https://wiki.mbalib.com/)
凸性(convexity)
目录 |
如果一种债券的市场价格等于它的面值,它的到期收益率就等于息票利率;如果市场价格高于(低于)面值,则到期收益率就会低于(高于)息票利率。据此,可以导出债券定价的两个基本特点:第一,如果债券价格上涨,则收益率必然下降,反之,如果债券价格下降,则收益率必然上升;第二,债券收益率的下降会引起债券价格的上升,且上升的幅度要超过债券收益率以同样比率上升引起的债券价格下降幅度。
根据第一条,债券价格与收益率呈反向关系;根据第二条,不仅表明二者的关系是非线性的,而且债券价格与收益率呈凸关系,这种关系常常被称为债券价格的凸性(convexity)。
凸性是指在某一到期收益率下,到期收益率发生变动而引起的价格变动幅度的变动程度。凸性是对债券价格曲线弯曲程度的一种度量。凸性的出现是为了弥补久期本身也会随着利率的变化而变化的不足。因为在利率变化比较大的情况下久期就不能完全描述债券价格对利率变动的敏感性。凸性越大,债券价格曲线弯曲程度越大,用修正久期度量债券的利率风险所产生的误差越大。
修正久期度量了收益率与债券价格的近似线性关系,即到期收益率变化时债券价格的稳定性。在同等要素条件下,修正久期小的债券较修正久期大的债券抗利率上升风险能力强,但抗利率下降风险能力较弱。
久期本身也会随着利率的变化而变化。所以它不能完全描述债券价格对利率变动的敏感性,1984年Stanley Diller引进凸性的概念。
久期描述了价格-收益率曲线的斜率,凸性描述了曲线的弯曲程度。凸性是债券价格对收益率的二阶导数。是对债券久期利率敏感性的测量。在价格-收益率出现大幅度变动时,它们的波动幅度呈非线性关系。由持久期作出的预测将有所偏离。凸性就是对这个偏离的修正。
凸性是对债券价格利率敏感性的二阶估计,是对债券久期利率敏感性的测量。在价格-收益率出现大幅度变动时,它们的波动幅度呈非线性关系。由持久期作出的预测将有所偏离。凸性就是对这个偏离的修正。无论收益率是上升还是下降,凸性所引起的修正都是正的。因此如果修正持久期相同,凸性越大越好。
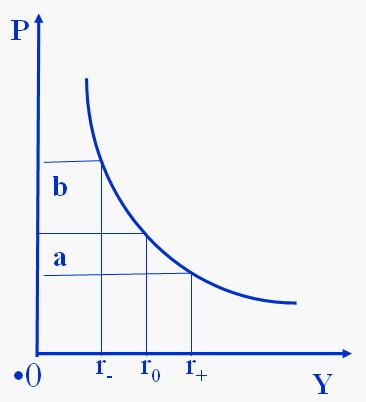
由债券定价定理1与4可知(更多债券定价定理,查看债券定价原理条目),债券价格-收益率曲线是一条从左上向右下倾斜,并且下凸的曲线。下图中b>a。
债券定价定理1:
债券价格与到期收益率成反向关系。
- 若到期收益率大于息票率,则债券价格低于面值,称为折价债券(discount bonds);
- 若到期收益率小于息票率,则债券价格高于面值,称为溢价债券(premium bonds);
- 若息票率等于到期收益率,则债券价格等于面值,称为平价债券(par bonds)。
对于可赎回债券,这一关系不成立。
债券定价定理4:
若债券期限一定,同等收益率变化下,债券收益率上升导致价格下跌的量,要小于收益率下降导致价格上升的量。
例:三债券的面值都为1000元,到期期限5年,息票率7%,当到期收益率变化时。
| 到期收益率(%) | 6 | 7 | 8 |
|---|---|---|---|
| 价格 | 1042.12 | 1000 | 960.07 |
| 债券价格变化率(%) | 4.21 | 0 | -4.00 |
1、凸性随久期的增加而增加。若收益率、久期不变,票面利率越大,凸性越大。利率下降时,凸性增加。
2、对于没有隐含期权的债券来说,凸性总大于0,即利率下降,债券价格将以加速度上升;当利率上升时,债券价格以减速度下降。
3、含有隐含期权的债券的凸性一般为负,即价格随着利率的下降以减速度上升,或债券的有效持续期随利率的下降而缩短,随利率的上升而延长。因为利率下降时买入期权的可能性增加了。
债券凸性投资价值的评估[1]
假设我们面对两个不同期次,具有相同存续期间的政府公债(无信用风险),两者的市场殖利率也正好相同,投资人对这两张债券是否会有不同的偏好呢?基于债券凸性的特质,如果两者有着不同的债券凸率,理性投资人应该会偏好债券凸率较高的公债。因此,在市场供给需求的调整下,我们可以预期两公债的殖利率必将有所调整,以反应投资人对高凸率公债的偏好。投资人对于高凸率债券的殖利率要求将会低于凸率较小的债券,也就是说,在其他条件相同的情况下,高凸率债券的价格应该比低凸率债券为高,以反应债券凸性的价值。
然而,市场中的债券价格果真有反应出债券凸性的价值吗?Kahn and Lochoff(1990)使用1981年至1986年的美国公债为样本,发现债券凸性在某些情况下会给投资人带来超额投资报酬,也就是说即使投资人以较高的价格购入具有高债券凸率的债券,其投资报酬仍然要比投资于低凸率债券为佳,这显示出交易市场对于债券凸性的定价并不正确,因此存在有超额获利空间。Lacey and Nawalkha(1993)则提出了不同的结论。这两位学者以1976到1987年的美国公债为样本作分析,结果并未发现高债券凸性会带给投资人超额的报酬,表示其已被市场正确的定价。
国内在此方面的实证研究也有不少,林聪钦(1995)以国内公债及公司债为样本,发现债券凸性对于超额投资报酬有解释能力,李耀宗(1995)针对国内公司债作分析,也发现债券凸性是超额投资报酬的解释因子之一,显示出针对债券凸性的操作策略是值得投资人重视的。吴荣昌(1997)使用1992到1996年国内所发行之35期次的政府公债,以时间序列进行横断面回归分析,来测试债券凸性以及其他因子解释债券超额报酬的能力。该研究结果发现,债券凸性在解释国内公债超额报酬的能力上并不显著,再度验证国内公债市场投资人对于债券凸性并未做出合理定价,这表示市场投资人或可针对债券凸性找出套利机会。
举例来说,投资人可以透过换券操作,在维持原有的存续期间条件下,将债券投资组合中低凸率债券换为高凸率债券,以获取更高的投资报酬。以市场中常见的平衡式操作法与单一式操作法为例,由于平衡式债券组合所产生的现金流量较为分散,在存续期间相同的情况下,要比单一式债券组合的凸率要高。如果国内公债市场果真对于凸率的定价不具效率,投资人可以在现有交易的各期次债券中,选取组成一个与目标债券存续期间相当的债券投资组合。由于债券组合之凸率较高,只要该组合的加权平均殖利率与目标债券的殖利率相当,投资人就可以享有更高的预期投资报酬率。而且即使该债券组合的殖利率要比目标债券为低,但是在考量债券凸性的价值后,其预期报酬率仍有可能会比较好.
债券凸性价值与利率波动[1]
债券凸性价值的存在是建基于未来利率的变动,利率变动幅度越大,债券凸性的价值就越高。而如果利率维持不变或变动幅度不 大,以债券凸性为主轴之操作策略效果是不易彰显的。然而,市场中常用的债券投资报酬衡量,包括殖利率(yield to maturity) ,以及持有期间报酬率(holding period return)等,均是假设利率结构曲线(yield curve)维持不变,利率波动幅度为零,这与实际市场情况大有出入。以一个目前市场殖利率为8%的债券而言,除非投资人持有该债券到期,而且在持有期间内该债券所产生之现金流量均可取得8%的再投资报酬率,否则投资人实际的报酬率将不会等于8%。换句话说,除非利率结构曲线不变,否则该债券的预期报酬率将不会等于殖利率,因此以殖利率为报酬衡量指标的投资决策容易产生偏误。
持有期间报酬率放宽了投资期间必须等于债券到期期限的限制,衡量投资人在预定之投资期限内的报酬。假设一个殖利率为8%的五年期债券,投资期限设为2年,则持有期间报酬率的计算就是依据这两年内之债券现金流量,加上两年后该债券的市场价值来决定。但是未来债券价值的计算仍是以在假设目前殖利率曲线维持不变的情形下所推估出来的远期利率(forwardrate)来决定。因此持有期间报酬率的正确性仍然取决于未来利率不变的假设。
实际的情况是,未来利率必定会有波动,如果投资人不将此因素纳入投资报酬的衡量过程,当然会产生决策上的误差,而由于债券凸性的存在,利率的波动将会提升债券的价值,因此持有期间报酬率会低估(under-estimate)债券的预期投资报酬率,而误差的部分就等于债券凸性的价值。
Ilmanen(1995)提出了一个将未来利率波动纳入考量的报酬衡量指标,我们称之为凸性调整后预期报酬(Convexity-adjusted expected return),该指标定义如 下:
凸性调整后预期报酬=持有期间报酬率+债券凸性价值
其中债券凸性价值的衡量是依据债券凸率(Conv)以及预期之殖利率波动程度(Vol(dy))计算如下:
债券凸性价值=![0.5\times Conv\times [Vol(dy)]^2](/w/images/math/3/5/4/354fad25ad774d2d830ed294a4da214c.png)
举例来说,如果投资人预期未来市场利率的上下波动幅度为50bp,对于一个凸率为10.75%的债券而言,其债券凸性价值为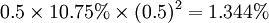 。假设该债券的预期持有期间报酬率为6.35%,则该债券之预期报酬应该是7.694%。以这样的方法来衡量不同债券的预期投债券凸性的进阶探讨资报酬将可以强化投资决策的正确性。在下表中,我们比较三个虚拟债券的投资决策,我们可以看到,在其他条件(例如信用风险等)相同情况下,如果单就持有期间报酬率来看,债券B应该是较佳的选择,但是如果将三个债券各自的债券凸性价值纳入考量,债券C反而是更佳之投资标的了。
。假设该债券的预期持有期间报酬率为6.35%,则该债券之预期报酬应该是7.694%。以这样的方法来衡量不同债券的预期投债券凸性的进阶探讨资报酬将可以强化投资决策的正确性。在下表中,我们比较三个虚拟债券的投资决策,我们可以看到,在其他条件(例如信用风险等)相同情况下,如果单就持有期间报酬率来看,债券B应该是较佳的选择,但是如果将三个债券各自的债券凸性价值纳入考量,债券C反而是更佳之投资标的了。
表(1):债券凸性调整后报酬率的比较:
| 债券 | 存续期间 | 债券凸率 | 预期持有期间报酬率 | 债券凸性价值 | 凸性调整后报酬率 |
| A | 3.5 | 12.58 | 7.35% | 1.57% | 8.92% |
| B | 3.5 | 10.25 | 7.43% | 1.28% | 8.71% |
| C | 3.5 | 14.37 | 7.16% | 1.80% | 8.96% |
*债券凸性价值的计算假设持有期间利率波动幅度为50bp。
我们可以看到,债券凸性价值的大小取决于两个因素:债券凸率以及利率波动性。一般而言,长期债券的凸率较小,但是短期利率波动性较高。此外,利率波动结构(volatility structure of interest rate, or volatility curve)也会随着市场情况而变动,这是投资人在估计利率波动程度时应该特别注意的地方。不过,即使短期利率波动较大,但是由于短期债券的凸率通常很小,即使忽略了债券凸性的考量,对于预期报酬的衡量影响不至于太大。对于长期债券而言,特别是在市场利率波动增较大时,债券凸性的重要性就不容忽视了。 Ilmanen(1995)提出一个简便的估计法,就是债券凸性价值随着债券存续期间的平方根增加。举例来说,凸率相同的两个债券,如果它们的存续期间分别为1及4,则两个债券凸性价值的差距大约为两倍。
债券凸性对利率曲线的影响[1]
除了对投资报酬率的影响之外,债券凸性对于利率期间结构曲线的影响也值得投资人注意。一般而言,市场中不同形状的利率期间结构曲线反应出了市场
投资人对于未来利率变动的预期。传统的预期理论(参见:凯恩斯的预期理论、纯粹预期理论),流动性溢酬理论(liquidity premium theory),以及市场区隔理论(Market segmentation theory)均对于殖利率曲线形状所代表的的内涵提出了解释,而投资人也据此来研拟各种不同的债券操作策略。例如根据即期利率曲线推估出远期利率(forward rate),以作为利率交换之定价依据,或者是根据所推估出远期利率结构曲线(forward rate curve)来作为利率模型的建构基础等等。
根据我们先前对债券凸性价值的分析,我们知道长期债券由于拥有较高的凸率,在其他条件相同情况下,应较具投资价值。因此,投资人对于长期债券的投资报酬率要求(不论是以殖利率或是持有期间报酬率来看)应该会比较低,以反应债券凸性的价值。如此一来,市场中的殖利率曲线将会随着债券凸性的进阶探讨债券期间的增长而产生向下弯曲(Inverted curve)的压力。我们可以用简单的预期理论为例子来说明。假设市场人士预期未来利率会逐渐上升,所观察到的殖利率结构曲线应该是一个向上攀升的曲线,但是由于长期债券的凸率较大,债券凸性价值较高,投资人对长期债券殖利率的要求降低,使得实际观察到的殖利率曲线会随着期间的增长而出现下滑的偏误,学术界将此现象称之为债券凸性偏误(Convexity bias)。如果我们不将债券凸性对利率曲线的影响纳入考量,而直接使用观察到的殖利率曲线做投资决策的依据,将会产生偏误。
以远期利率的估算为例,假设目前市场中所观察到的各期次即期利率为表(1)之第一行所示,而各期次债券所产生之凸性偏误值则显示在第三行。我可以依据凸性偏误值反推出真正的即期利率结构曲线,如表中之第四行。如果按照一般惯例使用利率预期理论来推估远期利率,我们可以看到,使用实际观察与修正后的即期利率所估计出来的远期利率(第二行及第五行)结果不大相同。在市场波动性较大时,此种差距会更为显著。
表(2):债券凸性偏误对远期利率估计之影响
| 期限 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 市场即期利率 | 5.00% | 5.15% | 5.30% | 5.40% | 5.48% | 5.55% | 5.60% | 5.64% |
| 估计之远期利率 | - | 5.30% | 5.60% | 5.70% | 5.80% | 5.90% | 5.90% | 5.92% |
| 凸性偏误 | 0.000% | 0.000% | 0.005% | 0.010% | 0.018% | 0.030% | 0.043% | 0.055% |
| 修正后即期利率 | 5.00% | 5.15% | 5.31% | 5.41% | 5.50% | 5.58% | 5.64% | 5.70% |
| 实际之远期利率 | - | 5.30% | 5.62% | 5.73% | 5.85% | 5.99% | 6.02% | 6.06% |
由于许多债券操作,例如利率交换交易等,需要正确的远期利率估计值来作为定价的基础,因此债券凸性偏误对于利率期间结构曲线的影响值得投资人注意。例如Burgharidt and Hoskins (1995)在一篇研究报告中就指出,市场人士惯用欧元期货价格来估计远期利率,以作为利率交换定价的基础。但是当市场利率波动增加时,由于利率交换价格具有债券凸性,而欧元期货的价格与报酬关系为线性(凸率为零),因此传统的市场操作方式会出现明显套利机会。简单来说,投资人只需要放空利率交换(也就是收固定利率,付浮动利率),并放空欧元期货来避险,便可以无风险的获取此凸性偏误的价值。由于该文比较偏重在衍生商品交易之应用,与本文主旨不尽相同,在此不做更进一步的介绍,有兴趣的读者可自行参阅该文。
本条目由以下用户参与贡献
Zfj3000,沙漠之鹰,funwmy,Vulture,Cabbage,Dan,Angle Roh,Yixi,风行水使,泡芙小姐,林巧玲,可恨密码记不住,连晓雾,Tracy,LuyinT,悠影,ElouiseLa.评论(共12条)
有點簡略了,是否可以更充實一點呢?因為凸性對於投資學來講是很重要的一項!
该内容已被Cabbage进行补充完善
哪里复制的 定理1下来就是定理4了
凸性是从债券的定价定理1和4得到的 所以定理1与定理4不是跳跃 是放上来补充解释凸性与债券定价的计算关系,可以参考库里债券定价原理条目,查看更多定理
凸性和票息率的关系到底是?投资组合书上说是inverse relationship,但是百科说的是正相关关系,到底是谁错了
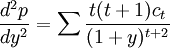
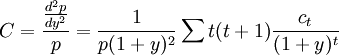






有點簡略了,是否可以更充實一點呢?因為凸性對於投資學來講是很重要的一項!